Question Number 119487 by liberty last updated on 25/Oct/20
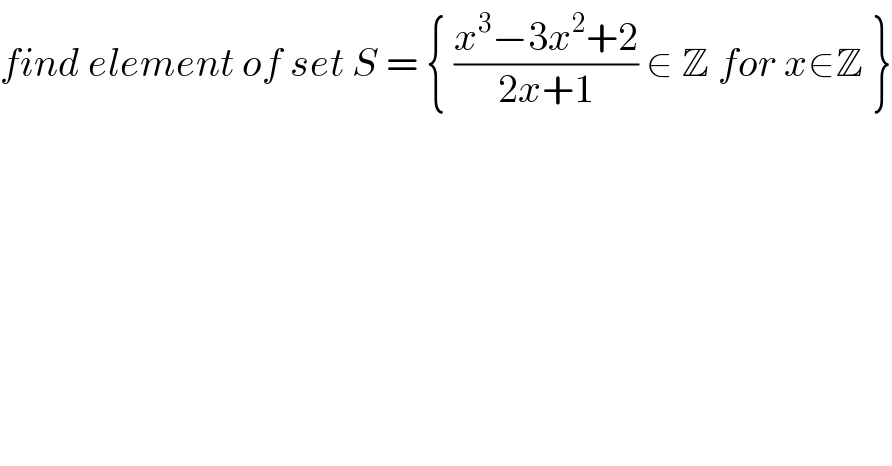
$${find}\:{element}\:{of}\:{set}\:{S}\:=\:\left\{\:\frac{{x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}}{\mathrm{2}{x}+\mathrm{1}}\:\in\:\mathbb{Z}\:{for}\:{x}\in\mathbb{Z}\:\right\} \\ $$
Answered by floor(10²Eta[1]) last updated on 25/Oct/20

$$\mathrm{2x}+\mathrm{1}\mid\mathrm{x}^{\mathrm{3}} −\mathrm{3x}^{\mathrm{2}} +\mathrm{2}\Leftrightarrow \\ $$$$\mathrm{2x}+\mathrm{1}\mid\mathrm{2}\left(\mathrm{x}^{\mathrm{3}} −\mathrm{3x}^{\mathrm{2}} +\mathrm{2}\right)−\mathrm{x}^{\mathrm{2}} \left(\mathrm{2x}+\mathrm{1}\right)=−\mathrm{7x}^{\mathrm{2}} +\mathrm{4} \\ $$$$\mathrm{2x}+\mathrm{1}\mid\mathrm{2}\left(−\mathrm{7x}^{\mathrm{2}} +\mathrm{4}\right)+\mathrm{7x}\left(\mathrm{2x}+\mathrm{1}\right)=\mathrm{7x}+\mathrm{8} \\ $$$$\mathrm{2x}+\mathrm{1}\mid\mathrm{2}\left(\mathrm{7x}+\mathrm{8}\right)−\mathrm{7}\left(\mathrm{2x}+\mathrm{1}\right)=\mathrm{9} \\ $$$$\mathrm{2x}+\mathrm{1}\in\left\{\pm\mathrm{1},\:\pm\mathrm{3},\:\pm\mathrm{9}\right\} \\ $$$$\mathrm{2x}+\mathrm{1}=\mathrm{1}\Rightarrow\mathrm{x}=\mathrm{0} \\ $$$$\mathrm{2x}+\mathrm{1}=−\mathrm{1}\Rightarrow\mathrm{x}=−\mathrm{1} \\ $$$$\mathrm{2x}+\mathrm{1}=\mathrm{3}\Rightarrow\mathrm{x}=\mathrm{1} \\ $$$$\mathrm{2x}+\mathrm{1}=−\mathrm{3}\Rightarrow\mathrm{x}=−\mathrm{2} \\ $$$$\mathrm{2x}+\mathrm{1}=\mathrm{9}\Rightarrow\mathrm{x}=\mathrm{4} \\ $$$$\mathrm{2x}+\mathrm{1}=−\mathrm{9}\Rightarrow\mathrm{x}=−\mathrm{5} \\ $$$$\mathrm{S}=\left\{−\mathrm{5},\:−\mathrm{2},\:−\mathrm{1},\:\mathrm{0},\:\mathrm{1},\:\mathrm{4}\right\} \\ $$
Answered by 1549442205PVT last updated on 25/Oct/20

$$\frac{{x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}}{\mathrm{2}{x}+\mathrm{1}}=\mathrm{k}\Rightarrow\frac{\mathrm{8x}^{\mathrm{3}} −\mathrm{24x}^{\mathrm{2}} +\mathrm{16}}{\mathrm{2x}+\mathrm{1}}=\mathrm{8k}\left(\mathrm{k}\in\mathrm{Z}\right) \\ $$$$\Leftrightarrow\mathrm{4x}^{\mathrm{2}} −\mathrm{14x}+\mathrm{7}−\frac{\mathrm{9}}{\mathrm{2x}+\mathrm{1}}=\mathrm{8k}\in\mathrm{Z}.\mathrm{Since}\:\mathrm{x}\in\mathrm{Z} \\ $$$$\Rightarrow\mathrm{2x}+\mathrm{1}\:\mid\mathrm{9}\Leftrightarrow\mathrm{2x}+\mathrm{1}\in\left\{\pm\mathrm{1},\pm\mathrm{3},\pm\mathrm{9}\right\} \\ $$$$\Leftrightarrow\mathrm{x}\in\left\{\mathrm{0},−\mathrm{1},\mathrm{1},−\mathrm{2},\mathrm{4},−\mathrm{5}\right\}.\mathrm{Checking}\:\mathrm{we}\: \\ $$$$\mathrm{obtain}\:\:\mathrm{k}=\left\{\mathrm{2},\mathrm{0},\mathrm{6},\mathrm{22}\right\}.\mathrm{Thus},\mathrm{S}\:\mathrm{has}\:\mathrm{four} \\ $$$$\mathrm{elements}\:\mathrm{are}\:\mathrm{S}=\left\{\mathrm{0},\mathrm{2},\mathrm{6},\mathrm{22}\right\} \\ $$
Commented by floor(10²Eta[1]) last updated on 25/Oct/20
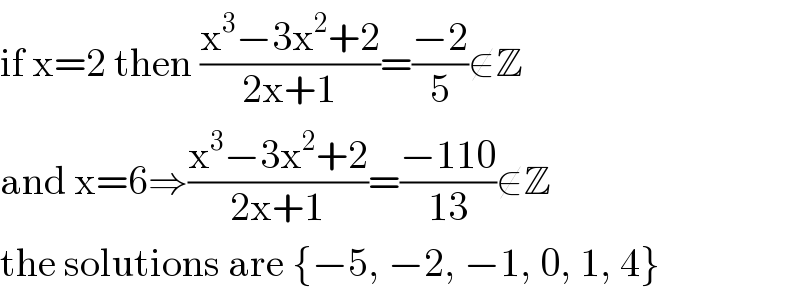
$$\mathrm{if}\:\mathrm{x}=\mathrm{2}\:\mathrm{then}\:\frac{\mathrm{x}^{\mathrm{3}} −\mathrm{3x}^{\mathrm{2}} +\mathrm{2}}{\mathrm{2x}+\mathrm{1}}=\frac{−\mathrm{2}}{\mathrm{5}}\notin\mathbb{Z} \\ $$$$\mathrm{and}\:\mathrm{x}=\mathrm{6}\Rightarrow\frac{\mathrm{x}^{\mathrm{3}} −\mathrm{3x}^{\mathrm{2}} +\mathrm{2}}{\mathrm{2x}+\mathrm{1}}=\frac{−\mathrm{110}}{\mathrm{13}}\notin\mathbb{Z} \\ $$$$\mathrm{the}\:\mathrm{solutions}\:\mathrm{are}\:\left\{−\mathrm{5},\:−\mathrm{2},\:−\mathrm{1},\:\mathrm{0},\:\mathrm{1},\:\mathrm{4}\right\} \\ $$
Commented by 1549442205PVT last updated on 25/Oct/20
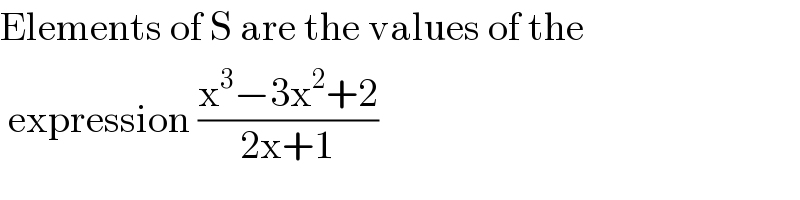
$$\mathrm{Elements}\:\mathrm{of}\:\mathrm{S}\:\mathrm{are}\:\mathrm{the}\:\mathrm{values}\:\mathrm{of}\:\mathrm{the} \\ $$$$\:\mathrm{expression}\:\frac{\mathrm{x}^{\mathrm{3}} −\mathrm{3x}^{\mathrm{2}} +\mathrm{2}}{\mathrm{2x}+\mathrm{1}} \\ $$
