Menu Close

Find-equation-of-a-plane-passing-through-the-points-x-1-y-1-z-1-x-2-y-2-z-2-and-perpendicular-to-the-plane-ax-by-cz-d-

Tinku Tara 0 Comments
Pin




Question Number 80943 by Kunal12588 last updated on 08/Feb/20
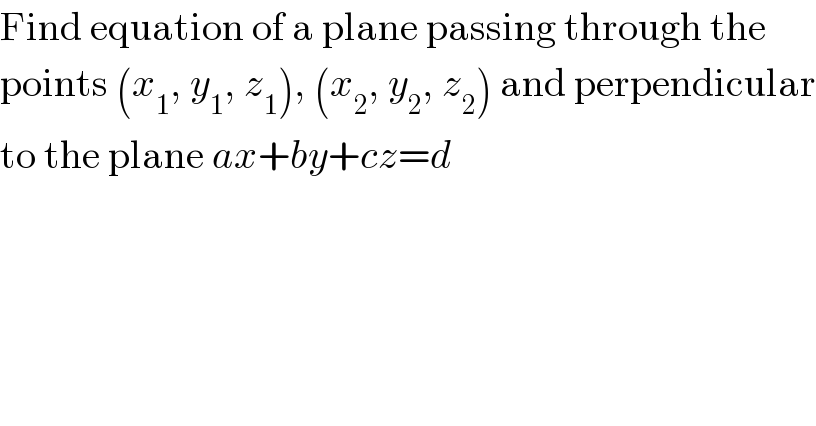
Find equation of a plane passing through the points (x_1 , y_1 , z_1 ), (x_2 , y_2 , z_2 ) and perpendicular to the plane ax+by+cz=d
$$\mathrm{Find}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{a}\:\mathrm{plane}\:\mathrm{passing}\:\mathrm{through}\:\mathrm{the} \\ $$$$\mathrm{points}\:\left({x}_{\mathrm{1}} ,\:{y}_{\mathrm{1}} ,\:{z}_{\mathrm{1}} \right),\:\left({x}_{\mathrm{2}} ,\:{y}_{\mathrm{2}} ,\:{z}_{\mathrm{2}} \right)\:\mathrm{and}\:\mathrm{perpendicular} \\ $$$$\mathrm{to}\:\mathrm{the}\:\mathrm{plane}\:{ax}+{by}+{cz}={d} \\ $$
Answered by mr W last updated on 08/Feb/20
say projection of P(x_1 ,y_1 ,z_1 ) an the plane ax+by+cz=d is P ′(x_3 ,y_3 ,z_3 ) x_3 =x_1 +at y_3 =y_1 +bt z_3 =z_1 +ct a(x_1 +at)+b(y_1 +bt)+c(z_1 +ct)=d ax_1 +by_1 +cz_1 +(a^2 +b^2 +c^2 )t=d ⇒t=((d−ax_1 −by_1 −cz_1 )/(a^2 +b^2 +c^2 )) ⇒x_3 =x_1 +((a(d−ax_1 −by_1 −cz_1 ))/(a^2 +b^2 +c^2 )) ⇒y_3 =y_1 +((b(d−ax_1 −by_1 −cz_1 ))/(a^2 +b^2 +c^2 )) ⇒z_3 =z_1 +((c(d−ax_1 −by_1 −cz_1 ))/(a^2 +b^2 +c^2 )) the requested plane passes through (x_1 ,y_1 ,z_1 ),(x_2 ,y_2 ,z_2 ),(x_3 ,y_3 ,z_3 ) and its equation is determinant (((x−x_1 ),(y−y_1 ),(z−z_1 )),((x_2 −x_1 ),(y_2 −y_1 ),(z_2 −z_1 )),((x_3 −x_1 ),(y_3 −y_1 ),(z_3 −z_1 )))=0 or determinant (((x−x_1 ),(y−y_1 ),(z−z_1 )),((x_2 −x_1 ),(y_2 −y_1 ),(z_2 −z_1 )),(((a(d−ax_1 −by_1 −cz_1 ))/(a^2 +b^2 +c^2 )),((b(d−ax_1 −by_1 −cz_1 ))/(a^2 +b^2 +c^2 )),((c(d−ax_1 −by_1 −cz_1 ))/(a^2 +b^2 +c^2 ))))=0
$${say}\:{projection}\:{of}\:{P}\left({x}_{\mathrm{1}} ,{y}_{\mathrm{1}} ,{z}_{\mathrm{1}} \right)\:{an}\:{the}\:{plane} \\ $$$${ax}+{by}+{cz}={d}\:{is}\:{P}\:'\left({x}_{\mathrm{3}} ,{y}_{\mathrm{3}} ,{z}_{\mathrm{3}} \right) \\ $$$${x}_{\mathrm{3}} ={x}_{\mathrm{1}} +{at} \\ $$$${y}_{\mathrm{3}} ={y}_{\mathrm{1}} +{bt} \\ $$$${z}_{\mathrm{3}} ={z}_{\mathrm{1}} +{ct} \\ $$$${a}\left({x}_{\mathrm{1}} +{at}\right)+{b}\left({y}_{\mathrm{1}} +{bt}\right)+{c}\left({z}_{\mathrm{1}} +{ct}\right)={d} \\ $$$${ax}_{\mathrm{1}} +{by}_{\mathrm{1}} +{cz}_{\mathrm{1}} +\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right){t}={d} \\ $$$$\Rightarrow{t}=\frac{{d}−{ax}_{\mathrm{1}} −{by}_{\mathrm{1}} −{cz}_{\mathrm{1}} }{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} } \\ $$$$\Rightarrow{x}_{\mathrm{3}} ={x}_{\mathrm{1}} +\frac{{a}\left({d}−{ax}_{\mathrm{1}} −{by}_{\mathrm{1}} −{cz}_{\mathrm{1}} \right)}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} } \\ $$$$\Rightarrow{y}_{\mathrm{3}} ={y}_{\mathrm{1}} +\frac{{b}\left({d}−{ax}_{\mathrm{1}} −{by}_{\mathrm{1}} −{cz}_{\mathrm{1}} \right)}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} } \\ $$$$\Rightarrow{z}_{\mathrm{3}} ={z}_{\mathrm{1}} +\frac{{c}\left({d}−{ax}_{\mathrm{1}} −{by}_{\mathrm{1}} −{cz}_{\mathrm{1}} \right)}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} } \\ $$$${the}\:{requested}\:{plane}\:{passes}\:{through} \\ $$$$\left({x}_{\mathrm{1}} ,{y}_{\mathrm{1}} ,{z}_{\mathrm{1}} \right),\left({x}_{\mathrm{2}} ,{y}_{\mathrm{2}} ,{z}_{\mathrm{2}} \right),\left({x}_{\mathrm{3}} ,{y}_{\mathrm{3}} ,{z}_{\mathrm{3}} \right)\:{and}\:{its} \\ $$$${equation}\:{is} \\ $$$$\begin{vmatrix}{{x}−{x}_{\mathrm{1}} }&{{y}−{y}_{\mathrm{1}} }&{{z}−{z}_{\mathrm{1}} }\\{{x}_{\mathrm{2}} −{x}_{\mathrm{1}} }&{{y}_{\mathrm{2}} −{y}_{\mathrm{1}} }&{{z}_{\mathrm{2}} −{z}_{\mathrm{1}} }\\{{x}_{\mathrm{3}} −{x}_{\mathrm{1}} }&{{y}_{\mathrm{3}} −{y}_{\mathrm{1}} }&{{z}_{\mathrm{3}} −{z}_{\mathrm{1}} }\end{vmatrix}=\mathrm{0} \\ $$$${or} \\ $$$$\begin{vmatrix}{{x}−{x}_{\mathrm{1}} }&{{y}−{y}_{\mathrm{1}} }&{{z}−{z}_{\mathrm{1}} }\\{{x}_{\mathrm{2}} −{x}_{\mathrm{1}} }&{{y}_{\mathrm{2}} −{y}_{\mathrm{1}} }&{{z}_{\mathrm{2}} −{z}_{\mathrm{1}} }\\{\frac{{a}\left({d}−{ax}_{\mathrm{1}} −{by}_{\mathrm{1}} −{cz}_{\mathrm{1}} \right)}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }}&{\frac{{b}\left({d}−{ax}_{\mathrm{1}} −{by}_{\mathrm{1}} −{cz}_{\mathrm{1}} \right)}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }}&{\frac{{c}\left({d}−{ax}_{\mathrm{1}} −{by}_{\mathrm{1}} −{cz}_{\mathrm{1}} \right)}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }}\end{vmatrix}=\mathrm{0} \\ $$
Commented by peter frank last updated on 08/Feb/20
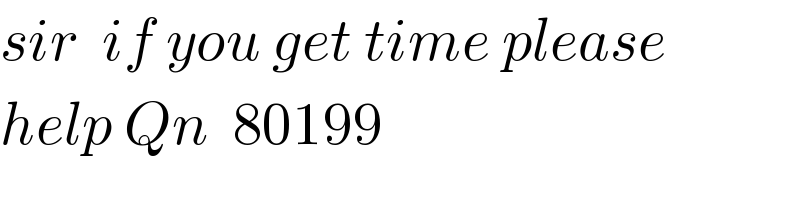
sir if you get time please help Qn 80199
$${sir}\:\:{if}\:{you}\:{get}\:{time}\:{please} \\ $$$${help}\:{Qn}\:\:\mathrm{80199} \\ $$
Commented by Kunal12588 last updated on 08/Feb/20
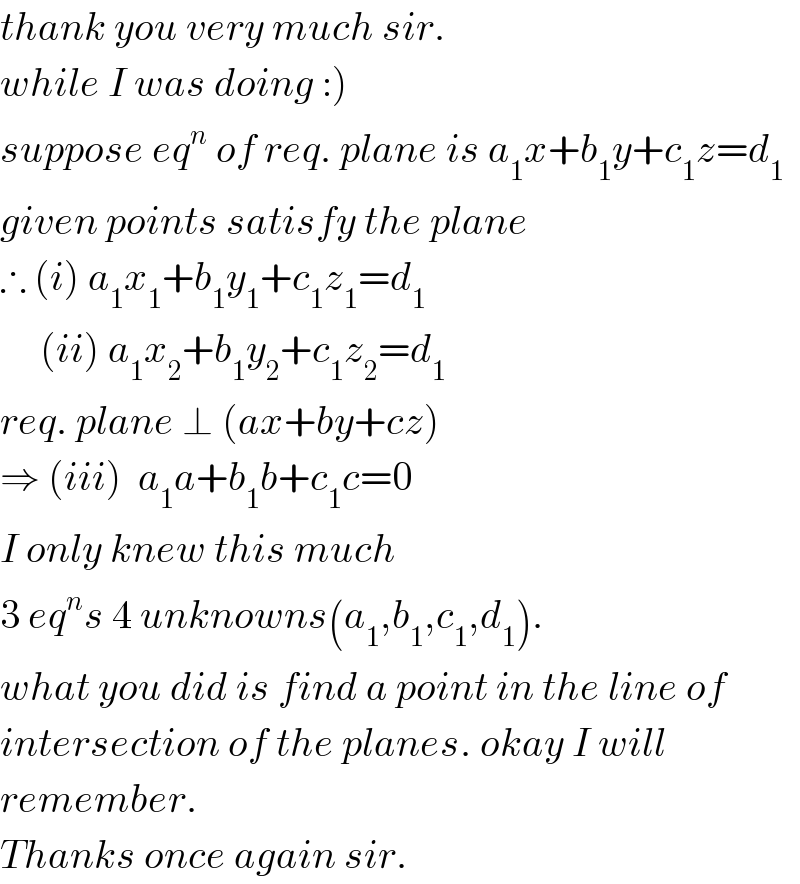
thank you very much sir. while I was doing :) suppose eq^n of req. plane is a_1 x+b_1 y+c_1 z=d_1 given points satisfy the plane ∴ (i) a_1 x_1 +b_1 y_1 +c_1 z_1 =d_1 (ii) a_1 x_2 +b_1 y_2 +c_1 z_2 =d_1 req. plane ⊥ (ax+by+cz) ⇒ (iii) a_1 a+b_1 b+c_1 c=0 I only knew this much 3 eq^n s 4 unknowns(a_1 ,b_1 ,c_1 ,d_1 ). what you did is find a point in the line of intersection of the planes. okay I will remember. Thanks once again sir.
$${thank}\:{you}\:{very}\:{much}\:{sir}. \\ $$$$\left.{while}\:{I}\:{was}\:{doing}\::\right) \\ $$$${suppose}\:{eq}^{{n}} \:{of}\:{req}.\:{plane}\:{is}\:{a}_{\mathrm{1}} {x}+{b}_{\mathrm{1}} {y}+{c}_{\mathrm{1}} {z}={d}_{\mathrm{1}} \\ $$$${given}\:{points}\:{satisfy}\:{the}\:{plane} \\ $$$$\therefore\:\left({i}\right)\:{a}_{\mathrm{1}} {x}_{\mathrm{1}} +{b}_{\mathrm{1}} {y}_{\mathrm{1}} +{c}_{\mathrm{1}} {z}_{\mathrm{1}} ={d}_{\mathrm{1}} \\ $$$$\:\:\:\:\:\left({ii}\right)\:{a}_{\mathrm{1}} {x}_{\mathrm{2}} +{b}_{\mathrm{1}} {y}_{\mathrm{2}} +{c}_{\mathrm{1}} {z}_{\mathrm{2}} ={d}_{\mathrm{1}} \\ $$$${req}.\:{plane}\:\bot\:\left({ax}+{by}+{cz}\right) \\ $$$$\Rightarrow\:\left({iii}\right)\:\:{a}_{\mathrm{1}} {a}+{b}_{\mathrm{1}} {b}+{c}_{\mathrm{1}} {c}=\mathrm{0} \\ $$$${I}\:{only}\:{knew}\:{this}\:{much}\: \\ $$$$\mathrm{3}\:{eq}^{{n}} {s}\:\mathrm{4}\:{unknowns}\left({a}_{\mathrm{1}} ,{b}_{\mathrm{1}} ,{c}_{\mathrm{1}} ,{d}_{\mathrm{1}} \right). \\ $$$${what}\:{you}\:{did}\:{is}\:{find}\:{a}\:{point}\:{in}\:{the}\:{line}\:{of} \\ $$$${intersection}\:{of}\:{the}\:{planes}.\:{okay}\:{I}\:{will} \\ $$$${remember}. \\ $$$${Thanks}\:{once}\:{again}\:{sir}. \\ $$
Commented by mr W last updated on 08/Feb/20
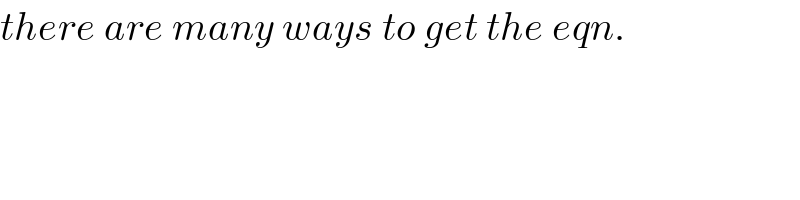
there are many ways to get the eqn.
$${there}\:{are}\:{many}\:{ways}\:{to}\:{get}\:{the}\:{eqn}. \\ $$
Commented by mr W last updated on 08/Feb/20
for the eqn. of the requested plane a_1 x+b_1 y+c_1 z=d_1 you actually only need to know the ratios of the coefficients, e.g. a_1 x+b_1 y+c_1 z=1 then you have three unknowns and three equations.
$${for}\:{the}\:{eqn}.\:{of}\:{the}\:{requested}\:\:{plane}\: \\ $$$${a}_{\mathrm{1}} {x}+{b}_{\mathrm{1}} {y}+{c}_{\mathrm{1}} {z}={d}_{\mathrm{1}} \\ $$$${you}\:{actually}\:{only}\:{need}\:{to}\:{know}\:{the} \\ $$$${ratios}\:{of}\:{the}\:{coefficients},\:{e}.{g}. \\ $$$${a}_{\mathrm{1}} {x}+{b}_{\mathrm{1}} {y}+{c}_{\mathrm{1}} {z}=\mathrm{1} \\ $$$${then}\:{you}\:{have}\:{three}\:{unknowns}\:{and} \\ $$$${three}\:{equations}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *