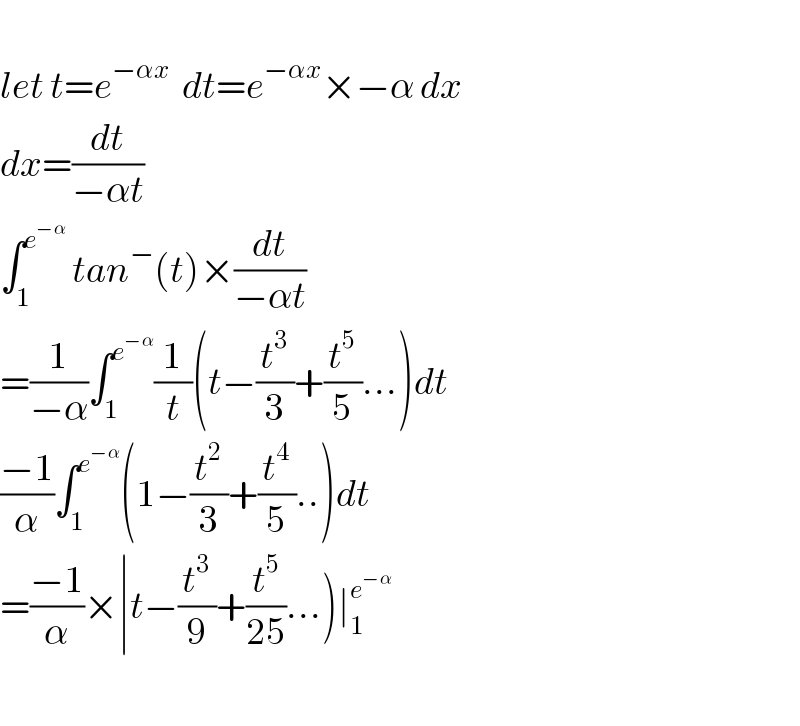Question Number 37888 by abdo mathsup 649 cc last updated on 19/Jun/18
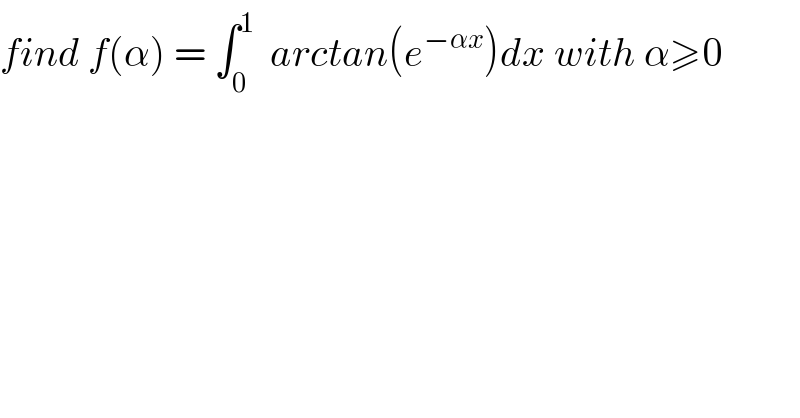
Commented by math khazana by abdo last updated on 21/Jun/18
![we have f^′ (α)=∫_0 ^1 ((−x e^(−αx) )/(1+e^(−2αx) ))dx = ∫_0 ^1 −x e^(−αx) { Σ_(n=0) ^∞ (−1)^n e^(−2nαx) } =Σ_(n=0) ^∞ (−1)^(n+1) ∫_0 ^1 x e^(−(2n+1)αx) dx but A_n =∫_0 ^1 x e^(−(2n+1)αx) dx=_((2n+1)αx=t) ∫_0 ^((2n+1)α) (t/((2n+1)α)) e^(−t) (dt/((2n+1)α)) = (1/((2n+1)^2 α^2 )) ∫_0 ^((2n+1)α) t .e^(−t) dt and by parts ∫_0 ^((2n+1)α) t.e^(−t) dt =[−t e^(−t) ]_0 ^((2n+1)α) +∫_0 ^((2n+1)α) e^(−t) dt =−(2n+1)α e^(−(2n+1)α) +[−e^(−t) ]_0 ^((2n+1)α) =−(2n+1)α e^(−(2n+1)α) +(1−e^(−(2n+1)α) ) ⇒ A_n = (1/((2n+1)^2 α^2 )){ −(2n+1)α e^(−(2n+1)α) +(1−e^(−(2n+1)α) ) =−(1/((2n+1)α)) e^(−(2n+1)α) +((1−e^(−(2n+1)α) )/((2n+1)^2 α^2 )) I =Σ_(n=0) ^∞ (((−1)^n )/((2n+1)α)) e^(−(2n+1)α) +Σ_(n=0) ^∞ (−1)^n ((e^(−(2n+1)α) −1)/((2n+1)^2 α^2 )) ...be continued...](https://www.tinkutara.com/question/Q38088.png)
Commented by math khazana by abdo last updated on 21/Jun/18
![we have artan^′ (u)= (1/(1+u^2 )) =Σ_(n=0) ^∞ (−1)^n u^(2n) ⇒ arctan(u) = Σ_(n=0) ^∞ (((−1)^n )/(2n+1)) u^(2n+1) +c (c=0)⇒ arctan(e^(−αx) ) =Σ_(n=0) ^∞ (((−1)^n )/(2n+1)) e^(−(2n+1)αx) and f(α)= ∫_0 ^1 arctan(e^(−αx) )dx =Σ_(n=0) ^∞ (((−1)^n )/(2n+1)) ∫_0 ^1 e^(−(2n+1)αx) dx =Σ_(n=0) ^∞ (((−1)^(n+1) )/((2n+1)^2 α))[ e^(−(2n+1)αx) ]_0 ^1 =(1/α) Σ_(n=0) ^∞ (((−1)^(n+1) )/((2n+1)^2 )){ e^(−(2n+1)α) −1} = (1/α) Σ_(n=0) ^∞ (((−1)^(n+1) )/((2n+1)^2 )) e^(−(2n+1)α) +(1/α) Σ_(n=0) ^∞ (((−1)^n )/((2n+1)^2 )) ...be continued...](https://www.tinkutara.com/question/Q38089.png)
Answered by tanmay.chaudhury50@gmail.com last updated on 21/Jun/18