Question Number 51825 by Abdo msup. last updated on 30/Dec/18
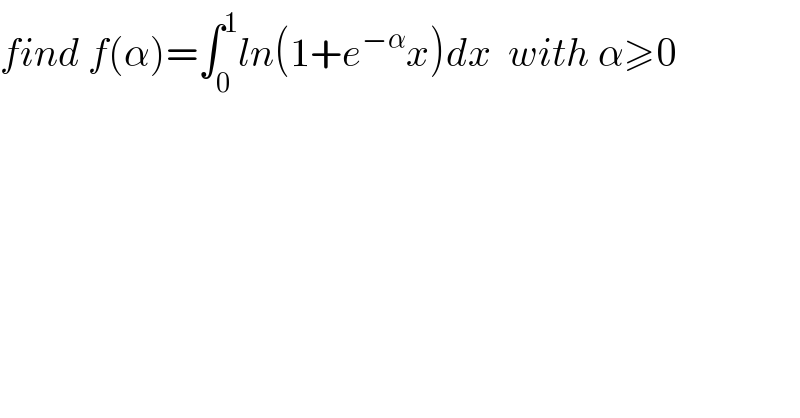
$${find}\:{f}\left(\alpha\right)=\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{e}^{−\alpha} {x}\right){dx}\:\:{with}\:\alpha\geqslant\mathrm{0} \\ $$
Commented by maxmathsup by imad last updated on 31/Dec/18
![let put e^(−α) =λ ⇒f(α)=∫_0 ^1 ln(1+λx)dx and by parts u^′ =1 ,v=ln(1+λx) we get f(α) =[xln(1+λx)]_0 ^1 −∫_0 ^1 x (λ/(1+λx))dx =ln(1+λ)−∫_0 ^1 ((λx+1−1)/(1+λx))dx =ln(1+λ)−1 +∫_0 ^1 (dx/(1+λx)) =ln(1+λ)−1 +(1/λ)ln∣1+λx∣ +c ⇒ f(α)=ln(1+e^(−α) )−1 +e^(−α) ln∣1+e^(−α) x∣ +c .](https://www.tinkutara.com/question/Q51891.png)
$${let}\:{put}\:{e}^{−\alpha} \:=\lambda\:\Rightarrow{f}\left(\alpha\right)=\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+\lambda{x}\right){dx}\:{and}\:{by}\:{parts}\:{u}^{'} =\mathrm{1}\:,{v}={ln}\left(\mathrm{1}+\lambda{x}\right) \\ $$$${we}\:{get}\:{f}\left(\alpha\right)\:=\left[{xln}\left(\mathrm{1}+\lambda{x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:−\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}\:\frac{\lambda}{\mathrm{1}+\lambda{x}}{dx} \\ $$$$={ln}\left(\mathrm{1}+\lambda\right)−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\lambda{x}+\mathrm{1}−\mathrm{1}}{\mathrm{1}+\lambda{x}}{dx}\:={ln}\left(\mathrm{1}+\lambda\right)−\mathrm{1}\:+\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dx}}{\mathrm{1}+\lambda{x}} \\ $$$$={ln}\left(\mathrm{1}+\lambda\right)−\mathrm{1}\:+\frac{\mathrm{1}}{\lambda}{ln}\mid\mathrm{1}+\lambda{x}\mid\:+{c}\:\Rightarrow \\ $$$${f}\left(\alpha\right)={ln}\left(\mathrm{1}+{e}^{−\alpha} \right)−\mathrm{1}\:+{e}^{−\alpha} {ln}\mid\mathrm{1}+{e}^{−\alpha} {x}\mid\:+{c}\:. \\ $$
Commented by maxmathsup by imad last updated on 31/Dec/18
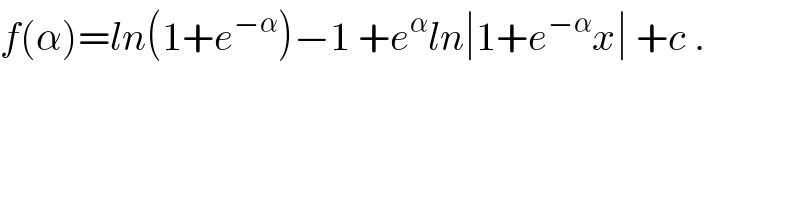
$${f}\left(\alpha\right)={ln}\left(\mathrm{1}+{e}^{−\alpha} \right)−\mathrm{1}\:+{e}^{\alpha} {ln}\mid\mathrm{1}+{e}^{−\alpha} {x}\mid\:+{c}\:. \\ $$
Commented by Abdo msup. last updated on 31/Dec/18
![f(α)=ln(1+λ)−1+[(1/λ)ln∣1+λx∣]_0 ^1 +c =ln(1+λ)−1 +(1/λ)ln(1+λ)+c ⇒f(α)=ln(1+e^(−α) )−1+e^α ln(1+e^(−α) )+c =(1+e^α )ln(1+e^(−α) )−1+c .](https://www.tinkutara.com/question/Q51900.png)
$${f}\left(\alpha\right)={ln}\left(\mathrm{1}+\lambda\right)−\mathrm{1}+\left[\frac{\mathrm{1}}{\lambda}{ln}\mid\mathrm{1}+\lambda{x}\mid\right]_{\mathrm{0}} ^{\mathrm{1}} \:+{c} \\ $$$$={ln}\left(\mathrm{1}+\lambda\right)−\mathrm{1}\:+\frac{\mathrm{1}}{\lambda}{ln}\left(\mathrm{1}+\lambda\right)+{c} \\ $$$$\Rightarrow{f}\left(\alpha\right)={ln}\left(\mathrm{1}+{e}^{−\alpha} \right)−\mathrm{1}+{e}^{\alpha} {ln}\left(\mathrm{1}+{e}^{−\alpha} \right)+{c} \\ $$$$=\left(\mathrm{1}+{e}^{\alpha} \right){ln}\left(\mathrm{1}+{e}^{−\alpha} \right)−\mathrm{1}+{c}\:\:. \\ $$
Answered by Smail last updated on 30/Dec/18
![let t=1+e^(−α) x⇒dx=e^α dt f(α)=e^α ∫_1 ^(1+e^(−α) ) ln(t)dt by parts u=ln(t)⇒u′=(1/t) v′=1⇒v=t f(α)=e^α [tlnt]_1 ^(1+e^(−α) ) −e^α ∫_1 ^(1+e^(−α) ) dt =e^α ((1+e^(−α) )ln(1+e^(−α) )−e^(−α) ) f(α)=(e^α +1)(ln(e^α +1)−α)−1](https://www.tinkutara.com/question/Q51833.png)
$${let}\:\:{t}=\mathrm{1}+{e}^{−\alpha} {x}\Rightarrow{dx}={e}^{\alpha} {dt} \\ $$$${f}\left(\alpha\right)={e}^{\alpha} \int_{\mathrm{1}} ^{\mathrm{1}+{e}^{−\alpha} } {ln}\left({t}\right){dt} \\ $$$${by}\:{parts} \\ $$$${u}={ln}\left({t}\right)\Rightarrow{u}'=\frac{\mathrm{1}}{{t}} \\ $$$${v}'=\mathrm{1}\Rightarrow{v}={t} \\ $$$${f}\left(\alpha\right)={e}^{\alpha} \left[{tlnt}\right]_{\mathrm{1}} ^{\mathrm{1}+{e}^{−\alpha} } −{e}^{\alpha} \int_{\mathrm{1}} ^{\mathrm{1}+{e}^{−\alpha} } {dt} \\ $$$$={e}^{\alpha} \left(\left(\mathrm{1}+{e}^{−\alpha} \right){ln}\left(\mathrm{1}+{e}^{−\alpha} \right)−{e}^{−\alpha} \right) \\ $$$${f}\left(\alpha\right)=\left({e}^{\alpha} +\mathrm{1}\right)\left({ln}\left({e}^{\alpha} +\mathrm{1}\right)−\alpha\right)−\mathrm{1} \\ $$
