Question Number 130532 by mathmax by abdo last updated on 26/Jan/21
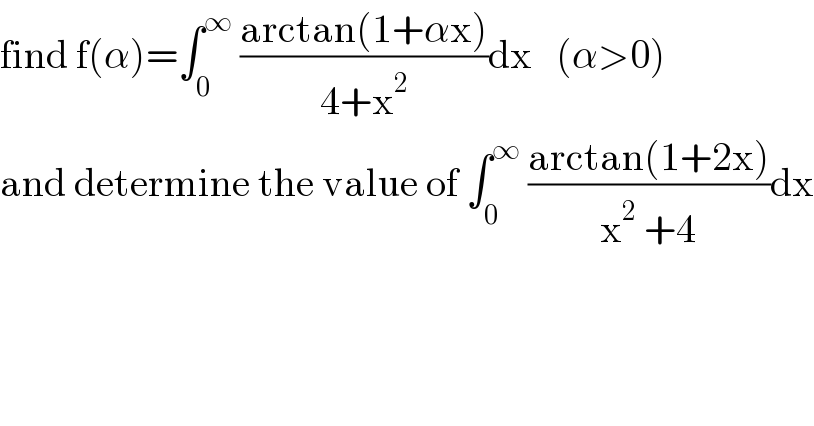
$$\mathrm{find}\:\mathrm{f}\left(\alpha\right)=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{arctan}\left(\mathrm{1}+\alpha\mathrm{x}\right)}{\mathrm{4}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:\:\:\left(\alpha>\mathrm{0}\right) \\ $$$$\mathrm{and}\:\mathrm{determine}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{arctan}\left(\mathrm{1}+\mathrm{2x}\right)}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{4}}\mathrm{dx} \\ $$
