Menu Close

find-f-0-arctan-x-1-x-2-dx-with-gt-0-

Tinku Tara 0 Comments
Pin




Question Number 50683 by maxmathsup by imad last updated on 18/Dec/18
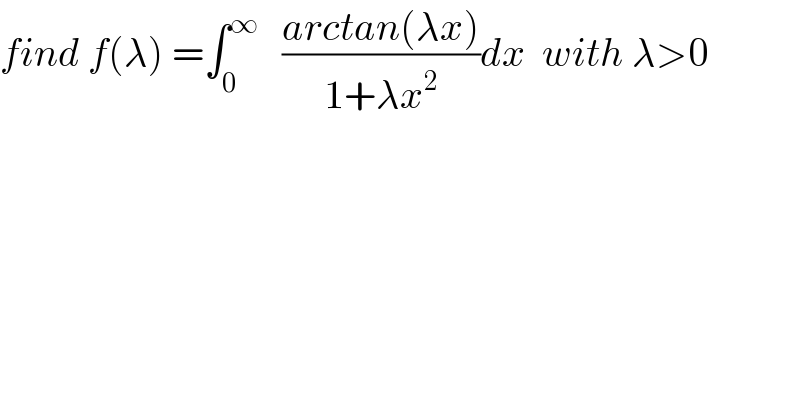
find f(λ) =∫_0 ^∞ ((arctan(λx))/(1+λx^2 ))dx with λ>0
$${find}\:{f}\left(\lambda\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{arctan}\left(\lambda{x}\right)}{\mathrm{1}+\lambda{x}^{\mathrm{2}} }{dx}\:\:{with}\:\lambda>\mathrm{0} \\ $$
Commented by Abdo msup. last updated on 21/Dec/18
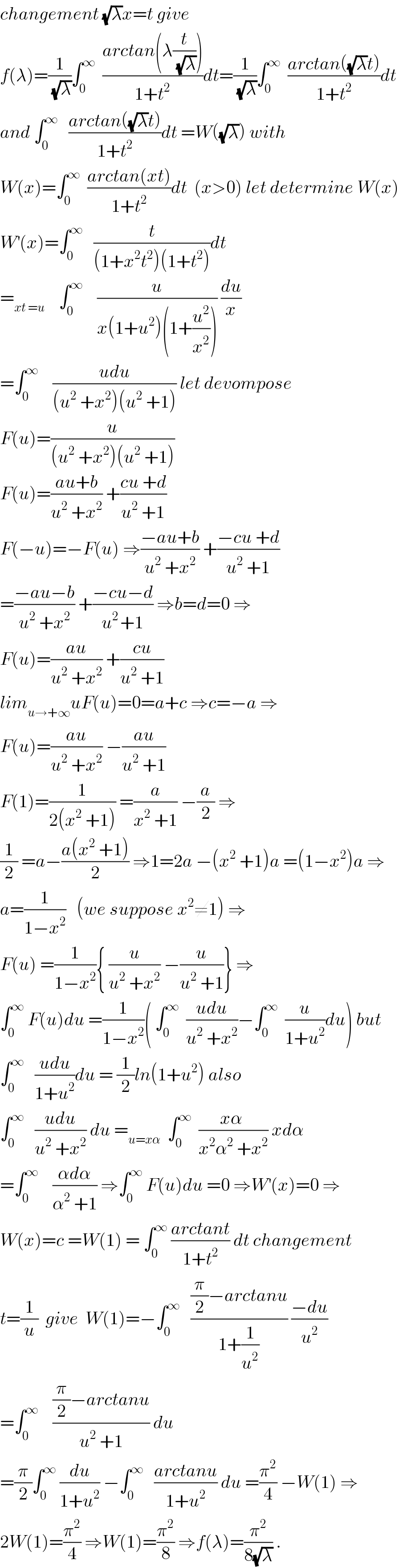
changement (√λ)x=t give f(λ)=(1/( (√λ)))∫_0 ^∞ ((arctan(λ(t/( (√λ)))))/(1+t^2 ))dt=(1/( (√λ)))∫_0 ^∞ ((arctan((√λ)t))/(1+t^2 ))dt and ∫_0 ^∞ ((arctan((√λ)t))/(1+t^2 ))dt =W((√λ)) with W(x)=∫_0 ^∞ ((arctan(xt))/(1+t^2 ))dt (x>0) let determine W(x) W^′ (x)=∫_0 ^∞ (t/((1+x^2 t^2 )(1+t^2 )))dt =_(xt =u) ∫_0 ^∞ (u/(x(1+u^2 )(1+(u^2 /x^2 )))) (du/x) =∫_0 ^∞ ((udu)/((u^2 +x^2 )(u^2 +1))) let devompose F(u)=(u/((u^2 +x^2 )(u^2 +1))) F(u)=((au+b)/(u^2 +x^2 )) +((cu +d)/(u^2 +1)) F(−u)=−F(u) ⇒((−au+b)/(u^2 +x^2 )) +((−cu +d)/(u^2 +1)) =((−au−b)/(u^2 +x^2 )) +((−cu−d)/(u^(2 ) +1)) ⇒b=d=0 ⇒ F(u)=((au)/(u^2 +x^2 )) +((cu)/(u^2 +1)) lim_(u→+∞) uF(u)=0=a+c ⇒c=−a ⇒ F(u)=((au)/(u^2 +x^2 )) −((au)/(u^2 +1)) F(1)=(1/(2(x^2 +1))) =(a/(x^2 +1)) −(a/2) ⇒ (1/2) =a−((a(x^2 +1))/2) ⇒1=2a −(x^2 +1)a =(1−x^2 )a ⇒ a=(1/(1−x^2 )) (we suppose x^2 ≠1) ⇒ F(u) =(1/(1−x^2 )){ (u/(u^2 +x^2 )) −(u/(u^2 +1))} ⇒ ∫_0 ^∞ F(u)du =(1/(1−x^2 ))( ∫_0 ^∞ ((udu)/(u^2 +x^2 ))−∫_0 ^∞ (u/(1+u^2 ))du) but ∫_0 ^∞ ((udu)/(1+u^2 ))du = (1/2)ln(1+u^2 ) also ∫_0 ^∞ ((udu)/(u^2 +x^2 )) du =_(u=xα) ∫_0 ^∞ ((xα )/(x^2 α^2 +x^2 )) xdα =∫_0 ^∞ ((αdα)/(α^2 +1)) ⇒∫_0 ^∞ F(u)du =0 ⇒W^′ (x)=0 ⇒ W(x)=c =W(1) = ∫_0 ^∞ ((arctant)/(1+t^2 )) dt changement t=(1/u) give W(1)=−∫_0 ^∞ (((π/2)−arctanu)/(1+(1/u^2 ))) ((−du)/u^2 ) =∫_0 ^∞ (((π/2)−arctanu)/(u^2 +1)) du =(π/2)∫_0 ^∞ (du/(1+u^2 )) −∫_0 ^∞ ((arctanu)/(1+u^2 )) du =(π^2 /4) −W(1) ⇒ 2W(1)=(π^2 /4) ⇒W(1)=(π^2 /8) ⇒f(λ)=(π^2 /(8(√λ))) .
$${changement}\:\sqrt{\lambda}{x}={t}\:{give} \\ $$$${f}\left(\lambda\right)=\frac{\mathrm{1}}{\:\sqrt{\lambda}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{{arctan}\left(\lambda\frac{{t}}{\:\sqrt{\lambda}}\right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}=\frac{\mathrm{1}}{\:\sqrt{\lambda}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{{arctan}\left(\sqrt{\lambda}{t}\right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$${and}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{arctan}\left(\sqrt{\lambda}{t}\right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\:={W}\left(\sqrt{\lambda}\right)\:{with} \\ $$$${W}\left({x}\right)=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{arctan}\left({xt}\right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\:\:\left({x}>\mathrm{0}\right)\:{let}\:{determine}\:{W}\left({x}\right) \\ $$$${W}^{'} \left({x}\right)=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{t}}{\left(\mathrm{1}+{x}^{\mathrm{2}} {t}^{\mathrm{2}} \right)\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{dt} \\ $$$$=_{{xt}\:={u}} \:\:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{u}}{{x}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\left(\mathrm{1}+\frac{{u}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\right)}\:\frac{{du}}{{x}} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{udu}}{\left({u}^{\mathrm{2}} \:+{x}^{\mathrm{2}} \right)\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)}\:{let}\:{devompose} \\ $$$${F}\left({u}\right)=\frac{{u}}{\left({u}^{\mathrm{2}} \:+{x}^{\mathrm{2}} \right)\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)} \\ $$$${F}\left({u}\right)=\frac{{au}+{b}}{{u}^{\mathrm{2}} \:+{x}^{\mathrm{2}} }\:+\frac{{cu}\:+{d}}{{u}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${F}\left(−{u}\right)=−{F}\left({u}\right)\:\Rightarrow\frac{−{au}+{b}}{{u}^{\mathrm{2}} \:+{x}^{\mathrm{2}} }\:+\frac{−{cu}\:+{d}}{{u}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$=\frac{−{au}−{b}}{{u}^{\mathrm{2}} \:+{x}^{\mathrm{2}} }\:+\frac{−{cu}−{d}}{{u}^{\mathrm{2}\:} +\mathrm{1}}\:\Rightarrow{b}={d}=\mathrm{0}\:\Rightarrow \\ $$$${F}\left({u}\right)=\frac{{au}}{{u}^{\mathrm{2}} \:+{x}^{\mathrm{2}} }\:+\frac{{cu}}{{u}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${lim}_{{u}\rightarrow+\infty} {uF}\left({u}\right)=\mathrm{0}={a}+{c}\:\Rightarrow{c}=−{a}\:\Rightarrow \\ $$$${F}\left({u}\right)=\frac{{au}}{{u}^{\mathrm{2}} \:+{x}^{\mathrm{2}} }\:−\frac{{au}}{{u}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${F}\left(\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{2}\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)}\:=\frac{{a}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:−\frac{{a}}{\mathrm{2}}\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\:={a}−\frac{{a}\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)}{\mathrm{2}}\:\Rightarrow\mathrm{1}=\mathrm{2}{a}\:−\left({x}^{\mathrm{2}} \:+\mathrm{1}\right){a}\:=\left(\mathrm{1}−{x}^{\mathrm{2}} \right){a}\:\Rightarrow \\ $$$${a}=\frac{\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} }\:\:\:\left({we}\:{suppose}\:{x}^{\mathrm{2}} \neq\mathrm{1}\right)\:\Rightarrow \\ $$$${F}\left({u}\right)\:=\frac{\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} }\left\{\:\frac{{u}}{{u}^{\mathrm{2}} \:+{x}^{\mathrm{2}} }\:−\frac{{u}}{{u}^{\mathrm{2}} \:+\mathrm{1}}\right\}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:{F}\left({u}\right){du}\:=\frac{\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} }\left(\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{udu}}{{u}^{\mathrm{2}} \:+{x}^{\mathrm{2}} }−\int_{\mathrm{0}} ^{\infty} \:\:\frac{{u}}{\mathrm{1}+{u}^{\mathrm{2}} }{du}\right)\:{but} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{udu}}{\mathrm{1}+{u}^{\mathrm{2}} }{du}\:=\:\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\:{also} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{udu}}{{u}^{\mathrm{2}} \:+{x}^{\mathrm{2}} }\:{du}\:=_{{u}={x}\alpha} \:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{x}\alpha\:}{{x}^{\mathrm{2}} \alpha^{\mathrm{2}} \:+{x}^{\mathrm{2}} }\:{xd}\alpha \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{\alpha{d}\alpha}{\alpha^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow\int_{\mathrm{0}} ^{\infty} \:{F}\left({u}\right){du}\:=\mathrm{0}\:\Rightarrow{W}^{'} \left({x}\right)=\mathrm{0}\:\Rightarrow \\ $$$${W}\left({x}\right)={c}\:={W}\left(\mathrm{1}\right)\:=\:\int_{\mathrm{0}} ^{\infty} \:\frac{{arctant}}{\mathrm{1}+{t}^{\mathrm{2}} }\:{dt}\:{changement} \\ $$$${t}=\frac{\mathrm{1}}{{u}}\:\:{give}\:\:{W}\left(\mathrm{1}\right)=−\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\frac{\pi}{\mathrm{2}}−{arctanu}}{\mathrm{1}+\frac{\mathrm{1}}{{u}^{\mathrm{2}} }}\:\frac{−{du}}{{u}^{\mathrm{2}} } \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{\frac{\pi}{\mathrm{2}}−{arctanu}}{{u}^{\mathrm{2}} \:+\mathrm{1}}\:{du} \\ $$$$=\frac{\pi}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\frac{{du}}{\mathrm{1}+{u}^{\mathrm{2}} }\:−\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{arctanu}}{\mathrm{1}+{u}^{\mathrm{2}} }\:{du}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{4}}\:−{W}\left(\mathrm{1}\right)\:\Rightarrow \\ $$$$\mathrm{2}{W}\left(\mathrm{1}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{4}}\:\Rightarrow{W}\left(\mathrm{1}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:\Rightarrow{f}\left(\lambda\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{8}\sqrt{\lambda}}\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *