Menu Close

find-f-0-pi-4-1-tant-dt-with-gt-0-also-calculate-0-pi-4-tant-1-tant-dt-

Tinku Tara 0 Comments
Pin




Question Number 51551 by maxmathsup by imad last updated on 28/Dec/18
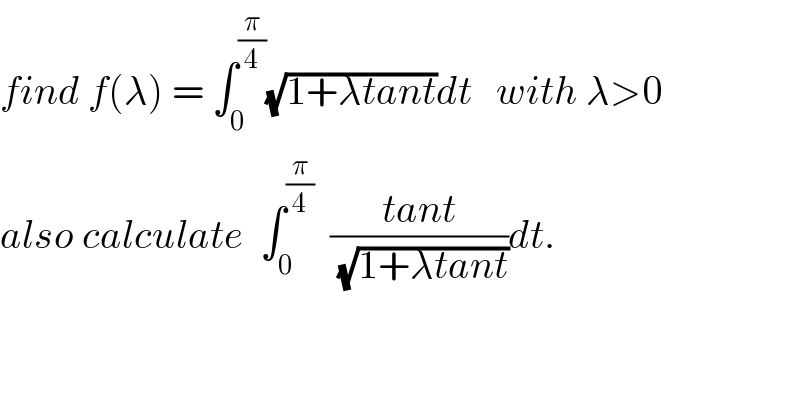
find f(λ) = ∫_0 ^(π/4) (√(1+λtant))dt with λ>0 also calculate ∫_0 ^(π/4) ((tant)/( (√(1+λtant))))dt.
$${find}\:{f}\left(\lambda\right)\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \sqrt{\mathrm{1}+\lambda{tant}}{dt}\:\:\:{with}\:\lambda>\mathrm{0} \\ $$$${also}\:{calculate}\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\frac{{tant}}{\:\sqrt{\mathrm{1}+\lambda{tant}}}{dt}. \\ $$
Commented by Abdo msup. last updated on 29/Dec/18
changement tant =x give f(λ) = ∫_0 ^1 (√(1+λx))(dx/(1+x^2 )) =∫_0 ^1 ((√(1+λx))/(1+x^2 ))dx =_(λx=sh^2 u) ∫_0 ^(argsh((√λ))) ((chu)/(1+(1/λ^2 )sh^4 u)) (1/λ) 2shuchu du =(2/λ) ∫_0 ^(ln((√λ)+(√(1+λ)))) ((sh(u)ch^2 (u))/(λ^2 +sh^4 u))λ^2 du =2λ ∫_0 ^(ln((√λ)+(√(1+λ)))) ((sh(u)((1+ch(2u))/2))/(λ^2 +(((ch(2u)−1)/2))^2 ))du =4λ ∫_0 ^(ln((√λ)+(√(1+λ)))) (((1+ch(2u))sh(u))/(4λ^2 +(ch(2u)−1)^2 ))du =4λ ∫_0 ^(ln((√λ)+(√(1+λ)))) (((1+((e^(2u) +e^(−2u) )/2))(((e^u −e^(−u) )/2)))/(4λ^2 +(((e^(2u) +e^(−2u) )/2)−1)^2 ))du =4λ ∫_0 ^(ln((√λ)+(√(1+λ)))) (((2+e^(2u) +e^(−2u) )(e^u −e^(−u) ))/(16λ^2 +(e^(2u) +e^(−2u) −2)^2 )) du =_(e^u =t) 4λ ∫_1 ^((√λ) +(√(1+λ))) (((2+t^2 +t^(−2) )(t−t^(−1) ))/(16λ^2 +(t^2 +t^(−2) −2)^2 )) (dt/t) =4λ ∫_1 ^((√λ)+(√(1+λ))) (((t^4 +2t^2 +1)(t^2 −1))/(t^4 (16λ^2 +(t^2 +t^(−2) −2)^2 )))dt ...be continued...
$${changement}\:{tant}\:={x}\:{give} \\ $$$${f}\left(\lambda\right)\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\sqrt{\mathrm{1}+\lambda{x}}\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} }\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{\sqrt{\mathrm{1}+\lambda{x}}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$=_{\lambda{x}={sh}^{\mathrm{2}} {u}} \:\:\:\:\int_{\mathrm{0}} ^{{argsh}\left(\sqrt{\lambda}\right)} \:\:\frac{{chu}}{\mathrm{1}+\frac{\mathrm{1}}{\lambda^{\mathrm{2}} }{sh}^{\mathrm{4}} {u}}\:\frac{\mathrm{1}}{\lambda}\:\mathrm{2}{shuchu}\:{du} \\ $$$$=\frac{\mathrm{2}}{\lambda}\:\int_{\mathrm{0}} ^{{ln}\left(\sqrt{\lambda}+\sqrt{\mathrm{1}+\lambda}\right)} \:\:\frac{{sh}\left({u}\right){ch}^{\mathrm{2}} \left({u}\right)}{\lambda^{\mathrm{2}} \:+{sh}^{\mathrm{4}} {u}}\lambda^{\mathrm{2}} {du} \\ $$$$=\mathrm{2}\lambda\:\int_{\mathrm{0}} ^{{ln}\left(\sqrt{\lambda}+\sqrt{\mathrm{1}+\lambda}\right)} \:\:\frac{{sh}\left({u}\right)\frac{\mathrm{1}+{ch}\left(\mathrm{2}{u}\right)}{\mathrm{2}}}{\lambda^{\mathrm{2}} \:+\left(\frac{{ch}\left(\mathrm{2}{u}\right)−\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }{du} \\ $$$$=\mathrm{4}\lambda\:\int_{\mathrm{0}} ^{{ln}\left(\sqrt{\lambda}+\sqrt{\mathrm{1}+\lambda}\right)} \:\:\frac{\left(\mathrm{1}+{ch}\left(\mathrm{2}{u}\right)\right){sh}\left({u}\right)}{\mathrm{4}\lambda^{\mathrm{2}} \:+\left({ch}\left(\mathrm{2}{u}\right)−\mathrm{1}\right)^{\mathrm{2}} }{du} \\ $$$$=\mathrm{4}\lambda\:\int_{\mathrm{0}} ^{{ln}\left(\sqrt{\lambda}+\sqrt{\mathrm{1}+\lambda}\right)} \:\:\:\frac{\left(\mathrm{1}+\frac{{e}^{\mathrm{2}{u}} \:+{e}^{−\mathrm{2}{u}} }{\mathrm{2}}\right)\left(\frac{{e}^{{u}} −{e}^{−{u}} }{\mathrm{2}}\right)}{\mathrm{4}\lambda^{\mathrm{2}} \:+\left(\frac{{e}^{\mathrm{2}{u}} \:+{e}^{−\mathrm{2}{u}} }{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{2}} }{du} \\ $$$$=\mathrm{4}\lambda\:\int_{\mathrm{0}} ^{{ln}\left(\sqrt{\lambda}+\sqrt{\mathrm{1}+\lambda}\right)} \:\:\:\:\:\frac{\left(\mathrm{2}+{e}^{\mathrm{2}{u}} \:+{e}^{−\mathrm{2}{u}} \right)\left({e}^{{u}} \:−{e}^{−{u}} \right)}{\mathrm{16}\lambda^{\mathrm{2}} \:+\left({e}^{\mathrm{2}{u}} \:+{e}^{−\mathrm{2}{u}} −\mathrm{2}\right)^{\mathrm{2}} }\:{du} \\ $$$$=_{{e}^{{u}} ={t}} \:\:\:\:\mathrm{4}\lambda\:\int_{\mathrm{1}} ^{\sqrt{\lambda}\:+\sqrt{\mathrm{1}+\lambda}} \:\:\:\frac{\left(\mathrm{2}+{t}^{\mathrm{2}} \:+{t}^{−\mathrm{2}} \right)\left({t}−{t}^{−\mathrm{1}} \right)}{\mathrm{16}\lambda^{\mathrm{2}} \:+\left({t}^{\mathrm{2}} \:+{t}^{−\mathrm{2}} −\mathrm{2}\right)^{\mathrm{2}} }\:\frac{{dt}}{{t}} \\ $$$$=\mathrm{4}\lambda\:\int_{\mathrm{1}} ^{\sqrt{\lambda}+\sqrt{\mathrm{1}+\lambda}} \:\:\:\frac{\left({t}^{\mathrm{4}} \:+\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{1}\right)\left({t}^{\mathrm{2}} −\mathrm{1}\right)}{{t}^{\mathrm{4}} \left(\mathrm{16}\lambda^{\mathrm{2}} \:+\left({t}^{\mathrm{2}} \:+{t}^{−\mathrm{2}} −\mathrm{2}\right)^{\mathrm{2}} \right)}{dt} \\ $$$$…{be}\:{continued}… \\ $$
Commented by Abdo msup. last updated on 29/Dec/18
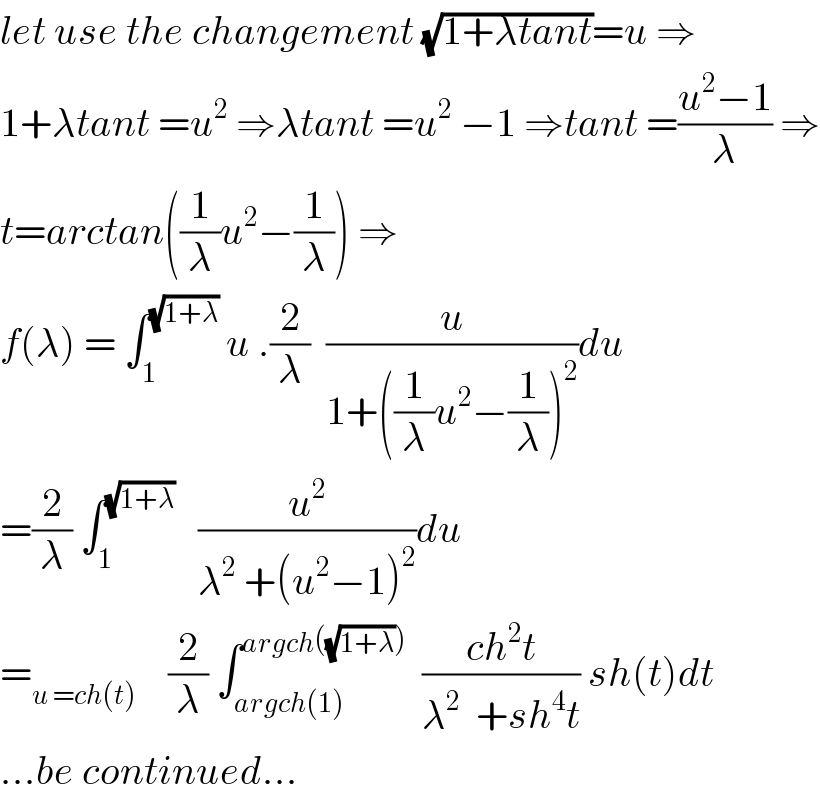
let use the changement (√(1+λtant))=u ⇒ 1+λtant =u^2 ⇒λtant =u^2 −1 ⇒tant =((u^2 −1)/λ) ⇒ t=arctan((1/λ)u^2 −(1/λ)) ⇒ f(λ) = ∫_1 ^(√(1+λ)) u .(2/λ) (u/(1+((1/λ)u^2 −(1/λ))^2 ))du =(2/λ) ∫_1 ^(√(1+λ)) (u^2 /(λ^2 +(u^2 −1)^2 ))du =_(u =ch(t)) (2/λ) ∫_(argch(1)) ^(argch((√(1+λ)))) ((ch^2 t)/(λ^2 +sh^4 t)) sh(t)dt ...be continued...
$${let}\:{use}\:{the}\:{changement}\:\sqrt{\mathrm{1}+\lambda{tant}}={u}\:\Rightarrow \\ $$$$\mathrm{1}+\lambda{tant}\:={u}^{\mathrm{2}} \:\Rightarrow\lambda{tant}\:={u}^{\mathrm{2}} \:−\mathrm{1}\:\Rightarrow{tant}\:=\frac{{u}^{\mathrm{2}} −\mathrm{1}}{\lambda}\:\Rightarrow \\ $$$${t}={arctan}\left(\frac{\mathrm{1}}{\lambda}{u}^{\mathrm{2}} −\frac{\mathrm{1}}{\lambda}\right)\:\Rightarrow \\ $$$${f}\left(\lambda\right)\:=\:\int_{\mathrm{1}} ^{\sqrt{\mathrm{1}+\lambda}} \:{u}\:.\frac{\mathrm{2}}{\lambda}\:\:\frac{{u}}{\mathrm{1}+\left(\frac{\mathrm{1}}{\lambda}{u}^{\mathrm{2}} −\frac{\mathrm{1}}{\lambda}\right)^{\mathrm{2}} }{du} \\ $$$$=\frac{\mathrm{2}}{\lambda}\:\int_{\mathrm{1}} ^{\sqrt{\mathrm{1}+\lambda}} \:\:\:\frac{{u}^{\mathrm{2}} }{\lambda^{\mathrm{2}} \:+\left({u}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }{du} \\ $$$$=_{{u}\:={ch}\left({t}\right)} \:\:\:\:\frac{\mathrm{2}}{\lambda}\:\int_{{argch}\left(\mathrm{1}\right)} ^{{argch}\left(\sqrt{\mathrm{1}+\lambda}\right)} \:\:\frac{{ch}^{\mathrm{2}} {t}}{\lambda^{\mathrm{2}} \:\:+{sh}^{\mathrm{4}} {t}}\:{sh}\left({t}\right){dt} \\ $$$$…{be}\:{continued}… \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 29/Dec/18
g(t)=(√(1+λtant)) g(0)=1 g((π/4))=(√(1+λ)) ∫_0 ^(π/4) (√(1+λtant)) dt≈(1/2)(1+(√(1+λ)) )×(π/4) ∫_0 ^(π/4) (√(1+λtant)) dt≈(π/8)(1+(√(1+λ)) )[approxmitation]
$${g}\left({t}\right)=\sqrt{\mathrm{1}+\lambda{tant}}\: \\ $$$${g}\left(\mathrm{0}\right)=\mathrm{1} \\ $$$${g}\left(\frac{\pi}{\mathrm{4}}\right)=\sqrt{\mathrm{1}+\lambda}\: \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \sqrt{\mathrm{1}+\lambda{tant}}\:{dt}\approx\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\sqrt{\mathrm{1}+\lambda}\:\right)×\frac{\pi}{\mathrm{4}} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \sqrt{\mathrm{1}+\lambda{tant}}\:{dt}\approx\frac{\pi}{\mathrm{8}}\left(\mathrm{1}+\sqrt{\mathrm{1}+\lambda}\:\right)\left[{approxmitation}\right] \\ $$$$ \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 29/Dec/18
g(t)=(√(1+λtant)) g(0)=1 g((π/4))=(√(1+λ)) ∫_0 ^(π/4) (√(1+λtant)) dt≈(1/2)(1+(√(1+λ)) )×(π/4) ∫_0 ^(π/4) (√(1+λtant)) dt≈(π/8)(1+(√(1+λ)) )[approxmitation]
$${g}\left({t}\right)=\sqrt{\mathrm{1}+\lambda{tant}}\: \\ $$$${g}\left(\mathrm{0}\right)=\mathrm{1} \\ $$$${g}\left(\frac{\pi}{\mathrm{4}}\right)=\sqrt{\mathrm{1}+\lambda}\: \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \sqrt{\mathrm{1}+\lambda{tant}}\:{dt}\approx\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\sqrt{\mathrm{1}+\lambda}\:\right)×\frac{\pi}{\mathrm{4}} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \sqrt{\mathrm{1}+\lambda{tant}}\:{dt}\approx\frac{\pi}{\mathrm{8}}\left(\mathrm{1}+\sqrt{\mathrm{1}+\lambda}\:\right)\left[{approxmitation}\right] \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *