Question Number 94214 by abony1303 last updated on 17/May/20

$${Find}\:{f}\left(\mathrm{0}\right)\:{when}\:{a}\:{polynomial}\:{f}\left({x}\right)\:{satisfies} \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{{f}\left({x}\right)}{{x}^{\mathrm{2}} −\mathrm{1}}=\mathrm{2} \\ $$$$\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}\:\:\frac{{f}\left({x}\right)}{{x}^{\mathrm{2}} −\mathrm{1}}=\mathrm{2}\:\: \\ $$$$\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\:\:\frac{{f}\left({x}\right)}{{x}^{\mathrm{4}} }\:=\mathrm{1}\:\:\:\:\:\:\:\:{pls}\:{Help}! \\ $$
Commented by john santu last updated on 17/May/20

$$\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\:\frac{\mathrm{f}\left(\mathrm{x}\right)}{\mathrm{x}^{\mathrm{4}} }\:=\:?? \\ $$
Commented by john santu last updated on 17/May/20

$$\mathrm{f}\left({x}\right)\:=\:\left({x}^{\mathrm{2}} −\mathrm{1}\right)\left({ax}^{\mathrm{2}} +{b}\right)\: \\ $$$$ \\ $$
Commented by abony1303 last updated on 17/May/20

$${changed} \\ $$
Commented by i jagooll last updated on 17/May/20
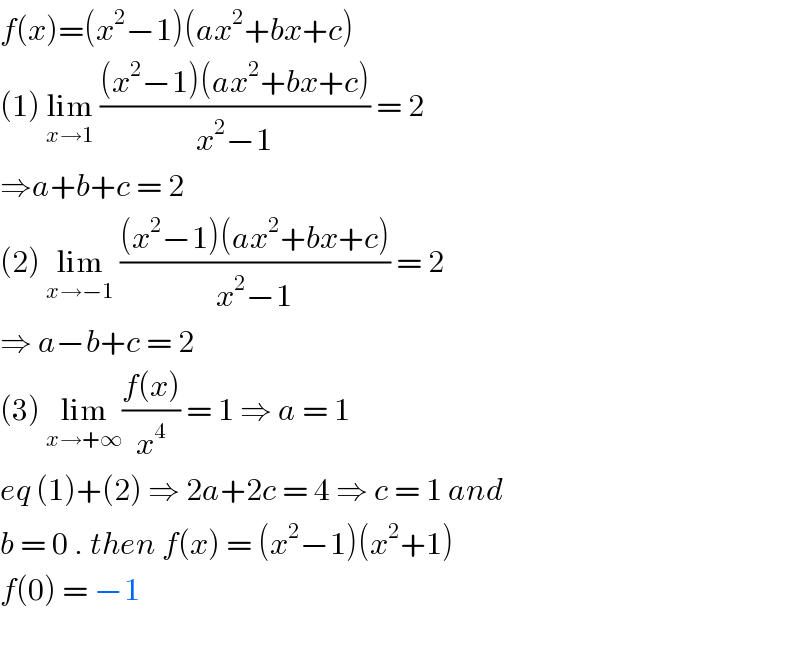
$${f}\left({x}\right)=\left({x}^{\mathrm{2}} −\mathrm{1}\right)\left({ax}^{\mathrm{2}} +{bx}+{c}\right) \\ $$$$\left(\mathrm{1}\right)\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\left({x}^{\mathrm{2}} −\mathrm{1}\right)\left({ax}^{\mathrm{2}} +{bx}+{c}\right)}{{x}^{\mathrm{2}} −\mathrm{1}}\:=\:\mathrm{2} \\ $$$$\Rightarrow{a}+{b}+{c}\:=\:\mathrm{2} \\ $$$$\left(\mathrm{2}\right)\:\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}\:\frac{\left({x}^{\mathrm{2}} −\mathrm{1}\right)\left({ax}^{\mathrm{2}} +{bx}+{c}\right)}{{x}^{\mathrm{2}} −\mathrm{1}}\:=\:\mathrm{2} \\ $$$$\Rightarrow\:{a}−{b}+{c}\:=\:\mathrm{2} \\ $$$$\left(\mathrm{3}\right)\:\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\frac{{f}\left({x}\right)}{{x}^{\mathrm{4}} }\:=\:\mathrm{1}\:\Rightarrow\:{a}\:=\:\mathrm{1}\: \\ $$$${eq}\:\left(\mathrm{1}\right)+\left(\mathrm{2}\right)\:\Rightarrow\:\mathrm{2}{a}+\mathrm{2}{c}\:=\:\mathrm{4}\:\Rightarrow\:{c}\:=\:\mathrm{1}\:{and}\: \\ $$$${b}\:=\:\mathrm{0}\:.\:{then}\:{f}\left({x}\right)\:=\:\left({x}^{\mathrm{2}} −\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$${f}\left(\mathrm{0}\right)\:=\:−\mathrm{1} \\ $$$$ \\ $$
