find-f-a-0-dx-x-3-a-3-with-a-gt-0-2-find-g-a-0-dx-x-3-a-3-2-3-find-the-value-of-0-dx-1-x-3-2-4-find-the-value-of-0-dx-8x-3-1-

Question Number 44202 by abdo.msup.com last updated on 23/Sep/18

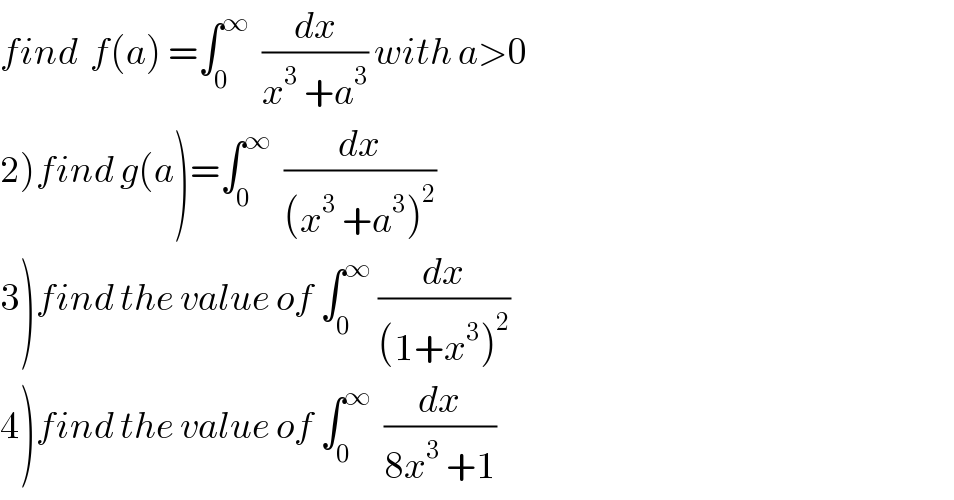
find f(a) =∫_0 ^∞ (dx/(x^3 +a^3 )) with a>0 2)find g(a)=∫_0 ^∞ (dx/((x^3 +a^3 )^2 )) 3)find the value of ∫_0 ^∞ (dx/((1+x^3 )^2 )) 4)find the value of ∫_0 ^∞ (dx/(8x^3 +1))

$${find}\:\:{f}\left({a}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{{x}^{\mathrm{3}} \:+{a}^{\mathrm{3}} }\:{with}\:{a}>\mathrm{0} \\ $$$$\left.\mathrm{2}\right){find}\:{g}\left({a}\right)=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{\left({x}^{\mathrm{3}} \:+{a}^{\mathrm{3}} \right)^{\mathrm{2}} } \\ $$$$\left.\mathrm{3}\right){find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\infty} \:\frac{{dx}}{\left(\mathrm{1}+{x}^{\mathrm{3}} \right)^{\mathrm{2}} } \\ $$$$\left.\mathrm{4}\right){find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{\mathrm{8}{x}^{\mathrm{3}} \:+\mathrm{1}} \\ $$

Commented by maxmathsup by imad last updated on 25/Sep/18

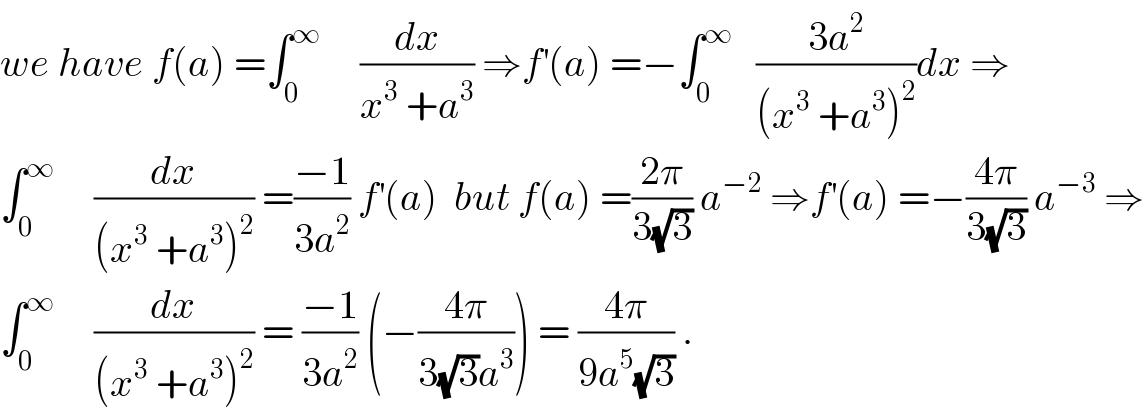
we have f(a) =∫_0 ^∞ (dx/(x^3 +a^3 )) ⇒f^′ (a) =−∫_0 ^∞ ((3a^2 )/((x^3 +a^3 )^2 ))dx ⇒ ∫_0 ^∞ (dx/((x^3 +a^3 )^2 )) =((−1)/(3a^2 )) f^′ (a) but f(a) =((2π)/(3(√3))) a^(−2) ⇒f^′ (a) =−((4π)/(3(√3))) a^(−3) ⇒ ∫_0 ^∞ (dx/((x^3 +a^3 )^2 )) = ((−1)/(3a^2 )) (−((4π)/(3(√3)a^3 ))) = ((4π)/(9a^5 (√3))) .

$${we}\:{have}\:{f}\left({a}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{{dx}}{{x}^{\mathrm{3}} \:+{a}^{\mathrm{3}} }\:\Rightarrow{f}^{'} \left({a}\right)\:=−\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{3}{a}^{\mathrm{2}} }{\left({x}^{\mathrm{3}} \:+{a}^{\mathrm{3}} \right)^{\mathrm{2}} }{dx}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{{dx}}{\left({x}^{\mathrm{3}} \:+{a}^{\mathrm{3}} \right)^{\mathrm{2}} }\:=\frac{−\mathrm{1}}{\mathrm{3}{a}^{\mathrm{2}} }\:{f}^{'} \left({a}\right)\:\:{but}\:{f}\left({a}\right)\:=\frac{\mathrm{2}\pi}{\mathrm{3}\sqrt{\mathrm{3}}}\:{a}^{−\mathrm{2}} \:\Rightarrow{f}^{'} \left({a}\right)\:=−\frac{\mathrm{4}\pi}{\mathrm{3}\sqrt{\mathrm{3}}}\:{a}^{−\mathrm{3}} \:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{{dx}}{\left({x}^{\mathrm{3}} \:+{a}^{\mathrm{3}} \right)^{\mathrm{2}} }\:=\:\frac{−\mathrm{1}}{\mathrm{3}{a}^{\mathrm{2}} }\:\left(−\frac{\mathrm{4}\pi}{\mathrm{3}\sqrt{\mathrm{3}}{a}^{\mathrm{3}} }\right)\:=\:\frac{\mathrm{4}\pi}{\mathrm{9}{a}^{\mathrm{5}} \sqrt{\mathrm{3}}}\:. \\ $$

Commented by maxmathsup by imad last updated on 25/Sep/18

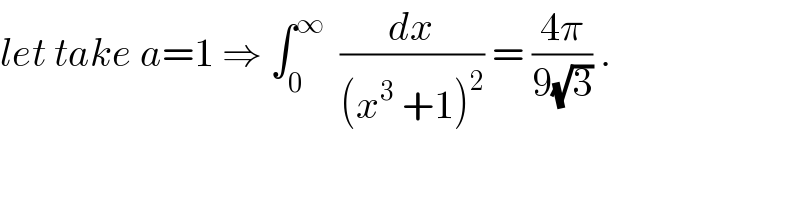
let take a=1 ⇒ ∫_0 ^∞ (dx/((x^3 +1)^2 )) = ((4π)/(9(√3))) .

$${let}\:{take}\:{a}=\mathrm{1}\:\Rightarrow\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{\left({x}^{\mathrm{3}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:=\:\frac{\mathrm{4}\pi}{\mathrm{9}\sqrt{\mathrm{3}}}\:. \\ $$

Commented by maxmathsup by imad last updated on 25/Sep/18

1) changement x =at give f(a) = ∫_0 ^∞ ((adt)/(a^3 (1+t^3 ))) =(1/a^2 ) ∫_0 ^∞ (dt/(t^3 +1)) let I =∫_0 ^∞ (dt/(t^3 +1)) ⇒ I =_(t=(1/u)) −∫_0 ^∞ (1/((1/u^3 ) +1)) ((−du)/u^2 ) =∫_0 ^∞ (du/((1/u) +u^2 )) =∫_0 ^∞ (u/(u^(3 ) +1)) du ⇒ 2I = ∫_0 ^∞ (dt/(t^3 +1)) +∫_0 ^∞ (t/(t^3 +1))dt =∫_0 ^∞ ((t+1)/(t^3 +1))dt =∫_0 ^∞ (dt/(t^2 −t +1)) = ∫_0 ^∞ (dt/((t−(1/2))^2 +(3/4))) =_(t−(1/2)=((√3)/2)u) (4/3)∫_(−(1/( (√3)))) ^(+∞) (1/(1+u^2 )) ((√3)/2)du = (2/( (√3))) ∫_(−(1/( (√3)))) ^(+∞) (du/(1+u^2 )) =(2/( (√3))) [arctan(u)]_(−((1 )/( (√3)))) ^(+∞) =(2/( (√3))){(π/2) +(π/6)}=(2/( (√3))) .((2π)/3) =((4π)/(3(√3))) ⇒ I = ((2π)/(3(√3))) ⇒f(a) = ((2π)/(3a^2 (√3))) .

$$\left.\mathrm{1}\right)\:{changement}\:{x}\:={at}\:{give}\:{f}\left({a}\right)\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{adt}}{{a}^{\mathrm{3}} \left(\mathrm{1}+{t}^{\mathrm{3}} \right)}\:=\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dt}}{{t}^{\mathrm{3}} \:+\mathrm{1}} \\ $$$${let}\:{I}\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dt}}{{t}^{\mathrm{3}} \:+\mathrm{1}}\:\Rightarrow\:{I}\:=_{{t}=\frac{\mathrm{1}}{{u}}} \:\:\:\:\:−\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{1}}{\frac{\mathrm{1}}{{u}^{\mathrm{3}} }\:+\mathrm{1}}\:\frac{−{du}}{{u}^{\mathrm{2}} }\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{du}}{\frac{\mathrm{1}}{{u}}\:+{u}^{\mathrm{2}} } \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{u}}{{u}^{\mathrm{3}\:} \:+\mathrm{1}}\:{du}\:\Rightarrow\:\mathrm{2}{I}\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{dt}}{{t}^{\mathrm{3}} \:+\mathrm{1}}\:+\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{t}}{{t}^{\mathrm{3}} \:+\mathrm{1}}{dt}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{t}+\mathrm{1}}{{t}^{\mathrm{3}} \:+\mathrm{1}}{dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dt}}{{t}^{\mathrm{2}} −{t}\:+\mathrm{1}}\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{{dt}}{\left({t}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{3}}{\mathrm{4}}}\:=_{{t}−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{u}} \:\:\frac{\mathrm{4}}{\mathrm{3}}\int_{−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{+\infty} \:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{2}} }\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{du} \\ $$$$=\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:\:\int_{−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{+\infty} \:\:\:\:\:\frac{{du}}{\mathrm{1}+{u}^{\mathrm{2}} }\:=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:\left[{arctan}\left({u}\right)\right]_{−\frac{\mathrm{1}\:}{\:\sqrt{\mathrm{3}}}} ^{+\infty} \:\:\:\:\:=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\left\{\frac{\pi}{\mathrm{2}}\:+\frac{\pi}{\mathrm{6}}\right\}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:.\frac{\mathrm{2}\pi}{\mathrm{3}}\:=\frac{\mathrm{4}\pi}{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow\:{I}\:=\:\frac{\mathrm{2}\pi}{\mathrm{3}\sqrt{\mathrm{3}}}\:\Rightarrow{f}\left({a}\right)\:=\:\frac{\mathrm{2}\pi}{\mathrm{3}{a}^{\mathrm{2}} \sqrt{\mathrm{3}}}\:. \\ $$

Commented by maxmathsup by imad last updated on 25/Sep/18

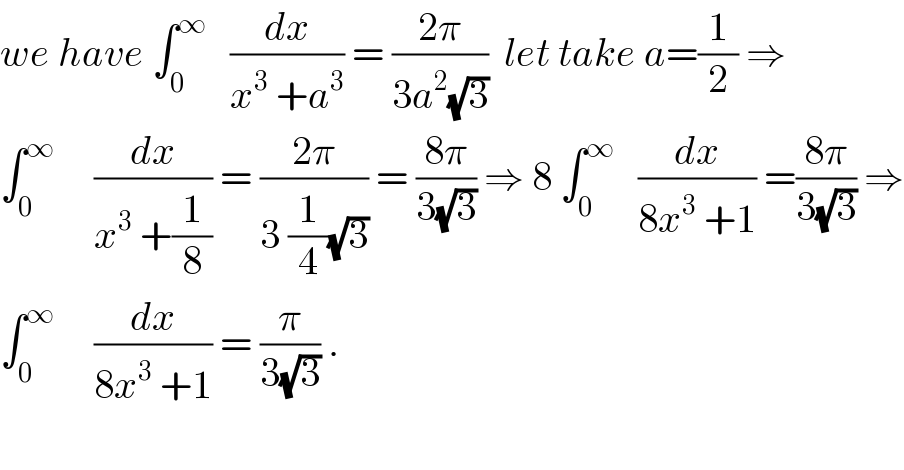
we have ∫_0 ^∞ (dx/(x^3 +a^3 )) = ((2π)/(3a^2 (√3))) let take a=(1/2) ⇒ ∫_0 ^∞ (dx/(x^3 +(1/8))) = ((2π)/(3 (1/4)(√3))) = ((8π)/(3(√3))) ⇒ 8 ∫_0 ^∞ (dx/(8x^3 +1)) =((8π)/(3(√3))) ⇒ ∫_0 ^∞ (dx/(8x^3 +1)) = (π/(3(√3))) .

$${we}\:{have}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dx}}{{x}^{\mathrm{3}} \:+{a}^{\mathrm{3}} }\:=\:\frac{\mathrm{2}\pi}{\mathrm{3}{a}^{\mathrm{2}} \sqrt{\mathrm{3}}}\:\:{let}\:{take}\:{a}=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\: \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{{dx}}{{x}^{\mathrm{3}} \:+\frac{\mathrm{1}}{\mathrm{8}}}\:=\:\frac{\mathrm{2}\pi}{\mathrm{3}\:\frac{\mathrm{1}}{\mathrm{4}}\sqrt{\mathrm{3}}}\:=\:\frac{\mathrm{8}\pi}{\mathrm{3}\sqrt{\mathrm{3}}}\:\Rightarrow\:\mathrm{8}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dx}}{\mathrm{8}{x}^{\mathrm{3}} \:+\mathrm{1}}\:=\frac{\mathrm{8}\pi}{\mathrm{3}\sqrt{\mathrm{3}}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{{dx}}{\mathrm{8}{x}^{\mathrm{3}} \:+\mathrm{1}}\:=\:\frac{\pi}{\mathrm{3}\sqrt{\mathrm{3}}}\:. \\ $$$$ \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 25/Sep/18

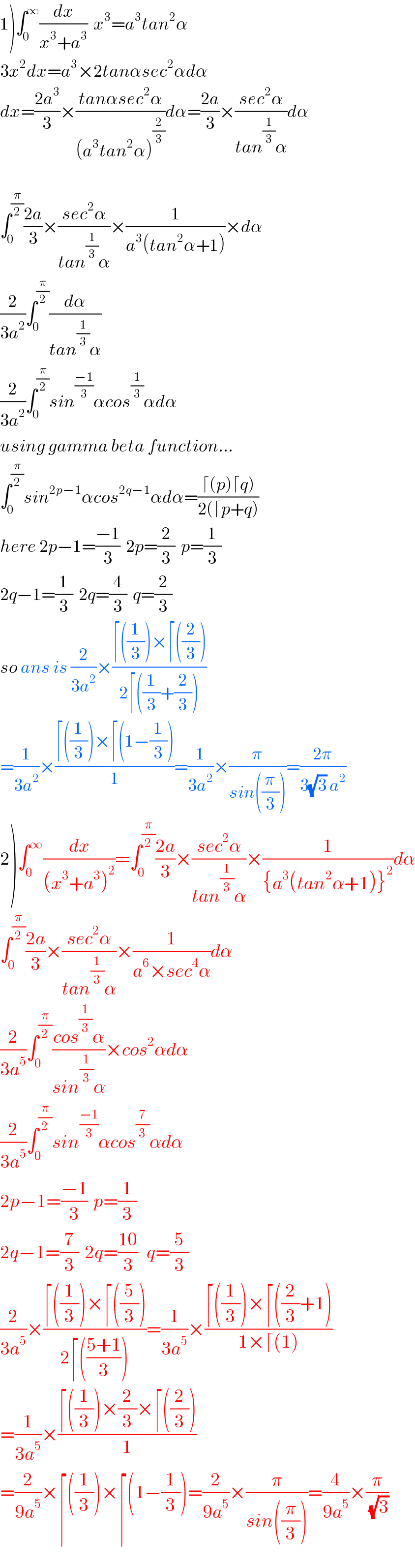
1)∫_0 ^∞ (dx/(x^3 +a^3 )) x^3 =a^3 tan^2 α 3x^2 dx=a^3 ×2tanαsec^2 αdα dx=((2a^3 )/3)×((tanαsec^2 α)/((a^3 tan^2 α)^(2/3) ))dα=((2a)/3)×((sec^2 α)/(tan^(1/3) α))dα ∫_0 ^(π/2) ((2a)/3)×((sec^2 α)/(tan^(1/3) α))×(1/(a^3 (tan^2 α+1)))×dα (2/(3a^2 ))∫_0 ^(π/2) (dα/(tan^(1/3) α)) (2/(3a^2 ))∫_0 ^(π/2) sin^((−1)/3) αcos^(1/3) αdα using gamma beta function... ∫_0 ^(π/2) sin^(2p−1) αcos^(2q−1) αdα=((⌈(p)⌈q))/(2(⌈p+q))) here 2p−1=((−1)/3) 2p=(2/3) p=(1/3) 2q−1=(1/3) 2q=(4/3) q=(2/3) so ans is (2/(3a^2 ))×((⌈((1/3))×⌈((2/3)))/(2⌈((1/3)+(2/3)))) =(1/(3a^2 ))×((⌈((1/3))×⌈(1−(1/3)))/1)=(1/(3a^2 ))×(π/(sin((π/3))))=((2π)/(3(√3) a^2 )) 2)∫_0 ^∞ (dx/((x^3 +a^3 )^2 ))=∫_0 ^(π/2) ((2a)/3)×((sec^2 α)/(tan^(1/3) α))×(1/({a^3 (tan^2 α+1)}^2 ))dα ∫_0 ^(π/2) ((2a)/3)×((sec^2 α)/(tan^(1/3) α))×(1/(a^6 ×sec^4 α))dα (2/(3a^5 ))∫_0 ^(π/2) ((cos^(1/3) α)/(sin^(1/3) α))×cos^2 αdα (2/(3a^5 ))∫_0 ^(π/2) sin^((−1)/3) αcos^(7/3) αdα 2p−1=((−1)/3) p=(1/3) 2q−1=(7/3) 2q=((10)/3) q=(5/3) (2/(3a^5 ))×((⌈((1/3))×⌈((5/3)))/(2⌈(((5+1)/3))))=(1/(3a^5 ))×((⌈((1/3))×⌈((2/3)+1))/(1×⌈(1))) =(1/(3a^5 ))×((⌈((1/3))×(2/3)×⌈((2/3)))/1) =(2/(9a^5 ))×⌈((1/3))×⌈(1−(1/3))=(2/(9a^5 ))×(π/(sin((π/3))))=(4/(9a^5 ))×(π/( (√3)))

$$\left.\mathrm{1}\right)\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{{x}^{\mathrm{3}} +{a}^{\mathrm{3}} }\:\:{x}^{\mathrm{3}} ={a}^{\mathrm{3}} {tan}^{\mathrm{2}} \alpha \\ $$$$\mathrm{3}{x}^{\mathrm{2}} {dx}={a}^{\mathrm{3}} ×\mathrm{2}{tan}\alpha{sec}^{\mathrm{2}} \alpha{d}\alpha \\ $$$${dx}=\frac{\mathrm{2}{a}^{\mathrm{3}} }{\mathrm{3}}×\frac{{tan}\alpha{sec}^{\mathrm{2}} \alpha}{\left({a}^{\mathrm{3}} {tan}^{\mathrm{2}} \alpha\right)^{\frac{\mathrm{2}}{\mathrm{3}}} }{d}\alpha=\frac{\mathrm{2}{a}}{\mathrm{3}}×\frac{{sec}^{\mathrm{2}} \alpha}{{tan}^{\frac{\mathrm{1}}{\mathrm{3}}} \alpha}{d}\alpha \\ $$$$ \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{2}{a}}{\mathrm{3}}×\frac{{sec}^{\mathrm{2}} \alpha}{{tan}^{\frac{\mathrm{1}}{\mathrm{3}}} \alpha}×\frac{\mathrm{1}}{{a}^{\mathrm{3}} \left({tan}^{\mathrm{2}} \alpha+\mathrm{1}\right)}×{d}\alpha \\ $$$$\frac{\mathrm{2}}{\mathrm{3}{a}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{d}\alpha}{{tan}^{\frac{\mathrm{1}}{\mathrm{3}}} \alpha} \\ $$$$\frac{\mathrm{2}}{\mathrm{3}{a}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}^{\frac{−\mathrm{1}}{\mathrm{3}}} \alpha{cos}^{\frac{\mathrm{1}}{\mathrm{3}}} \alpha{d}\alpha \\ $$$${using}\:{gamma}\:{beta}\:{function}… \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}^{\mathrm{2}{p}−\mathrm{1}} \alpha{cos}^{\mathrm{2}{q}−\mathrm{1}} \alpha{d}\alpha=\frac{\left.\lceil\left({p}\right)\lceil{q}\right)}{\mathrm{2}\left(\lceil{p}+{q}\right)} \\ $$$${here}\:\mathrm{2}{p}−\mathrm{1}=\frac{−\mathrm{1}}{\mathrm{3}}\:\:\mathrm{2}{p}=\frac{\mathrm{2}}{\mathrm{3}}\:\:{p}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\mathrm{2}{q}−\mathrm{1}=\frac{\mathrm{1}}{\mathrm{3}}\:\:\mathrm{2}{q}=\frac{\mathrm{4}}{\mathrm{3}}\:\:{q}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$${so}\:{ans}\:{is}\:\frac{\mathrm{2}}{\mathrm{3}{a}^{\mathrm{2}} }×\frac{\lceil\left(\frac{\mathrm{1}}{\mathrm{3}}\right)×\lceil\left(\frac{\mathrm{2}}{\mathrm{3}}\right)}{\mathrm{2}\lceil\left(\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{2}}{\mathrm{3}}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}{a}^{\mathrm{2}} }×\frac{\lceil\left(\frac{\mathrm{1}}{\mathrm{3}}\right)×\lceil\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}\right)}{\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{3}{a}^{\mathrm{2}} }×\frac{\pi}{{sin}\left(\frac{\pi}{\mathrm{3}}\right)}=\frac{\mathrm{2}\pi}{\mathrm{3}\sqrt{\mathrm{3}}\:{a}^{\mathrm{2}} } \\ $$$$\left.\mathrm{2}\right)\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{\left({x}^{\mathrm{3}} +{a}^{\mathrm{3}} \right)^{\mathrm{2}} }=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{2}{a}}{\mathrm{3}}×\frac{{sec}^{\mathrm{2}} \alpha}{{tan}^{\frac{\mathrm{1}}{\mathrm{3}}} \alpha}×\frac{\mathrm{1}}{\left\{{a}^{\mathrm{3}} \left({tan}^{\mathrm{2}} \alpha+\mathrm{1}\right)\right\}^{\mathrm{2}} }{d}\alpha \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{2}{a}}{\mathrm{3}}×\frac{{sec}^{\mathrm{2}} \alpha}{{tan}^{\frac{\mathrm{1}}{\mathrm{3}}} \alpha}×\frac{\mathrm{1}}{{a}^{\mathrm{6}} ×{sec}^{\mathrm{4}} \alpha}{d}\alpha \\ $$$$\frac{\mathrm{2}}{\mathrm{3}{a}^{\mathrm{5}} }\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{cos}^{\frac{\mathrm{1}}{\mathrm{3}}} \alpha}{{sin}^{\frac{\mathrm{1}}{\mathrm{3}}} \alpha}×{cos}^{\mathrm{2}} \alpha{d}\alpha \\ $$$$\frac{\mathrm{2}}{\mathrm{3}{a}^{\mathrm{5}} }\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}^{\frac{−\mathrm{1}}{\mathrm{3}}} \alpha{cos}^{\frac{\mathrm{7}}{\mathrm{3}}} \alpha{d}\alpha \\ $$$$\mathrm{2}{p}−\mathrm{1}=\frac{−\mathrm{1}}{\mathrm{3}}\:\:{p}=\frac{\mathrm{1}}{\mathrm{3}}\:\: \\ $$$$\mathrm{2}{q}−\mathrm{1}=\frac{\mathrm{7}}{\mathrm{3}}\:\:\mathrm{2}{q}=\frac{\mathrm{10}}{\mathrm{3}}\:\:\:{q}=\frac{\mathrm{5}}{\mathrm{3}} \\ $$$$\frac{\mathrm{2}}{\mathrm{3}{a}^{\mathrm{5}} }×\frac{\lceil\left(\frac{\mathrm{1}}{\mathrm{3}}\right)×\lceil\left(\frac{\mathrm{5}}{\mathrm{3}}\right)}{\mathrm{2}\lceil\left(\frac{\mathrm{5}+\mathrm{1}}{\mathrm{3}}\right)}=\frac{\mathrm{1}}{\mathrm{3}{a}^{\mathrm{5}} }×\frac{\lceil\left(\frac{\mathrm{1}}{\mathrm{3}}\right)×\lceil\left(\frac{\mathrm{2}}{\mathrm{3}}+\mathrm{1}\right)}{\mathrm{1}×\lceil\left(\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}{a}^{\mathrm{5}} }×\frac{\lceil\left(\frac{\mathrm{1}}{\mathrm{3}}\right)×\frac{\mathrm{2}}{\mathrm{3}}×\lceil\left(\frac{\mathrm{2}}{\mathrm{3}}\right)}{\mathrm{1}} \\ $$$$=\frac{\mathrm{2}}{\mathrm{9}{a}^{\mathrm{5}} }×\lceil\left(\frac{\mathrm{1}}{\mathrm{3}}\right)×\lceil\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}\right)=\frac{\mathrm{2}}{\mathrm{9}{a}^{\mathrm{5}} }×\frac{\pi}{{sin}\left(\frac{\pi}{\mathrm{3}}\right)}=\frac{\mathrm{4}}{\mathrm{9}{a}^{\mathrm{5}} }×\frac{\pi}{\:\sqrt{\mathrm{3}}} \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 25/Sep/18