Question Number 44175 by abdo.msup.com last updated on 22/Sep/18
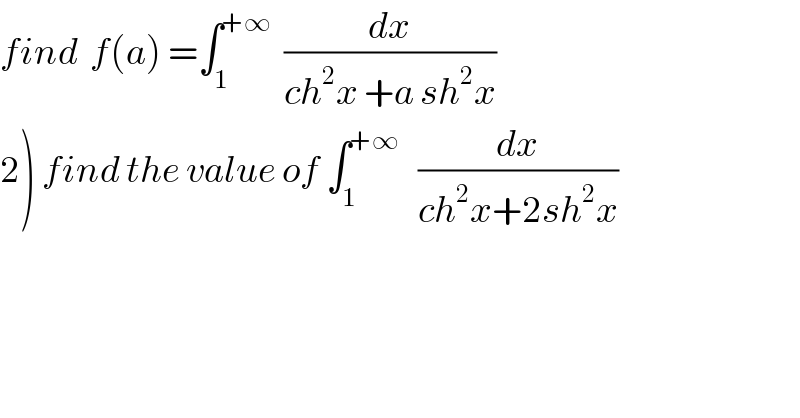
$${find}\:\:{f}\left({a}\right)\:=\int_{\mathrm{1}} ^{+\infty} \:\:\frac{{dx}}{{ch}^{\mathrm{2}} {x}\:+{a}\:{sh}^{\mathrm{2}} {x}} \\ $$$$\left.\mathrm{2}\right)\:{find}\:{the}\:{value}\:{of}\:\int_{\mathrm{1}} ^{+\infty} \:\:\:\frac{{dx}}{{ch}^{\mathrm{2}} {x}+\mathrm{2}{sh}^{\mathrm{2}} {x}} \\ $$
Commented by maxmathsup by imad last updated on 24/Sep/18
![1) we have f(a)= ∫_1 ^(+∞) (dx/(((1+ch(2x))/2) +a ((ch(2x)−1)/2))) = ∫_1 ^(+∞) ((2dx)/(1+ch(2x)+ach(2x)−a)) = ∫_1 ^(+∞) ((2dx)/((1+a)ch(2x) +1−a)) = ∫_1 ^(+∞) ((2dx)/((1+a)((e^(2x) +e^(−2x) )/2) +1−a)) =∫_1 ^(+∞) ((4dx)/((1+a)(e^(2x) +e^(−2x) ) +2−2a)) =_(e^(2x) =t) ∫_e^2 ^(+∞) (4/((1+a)(t+t^(−1) ) +2−2a)) (dt/(2t)) = ∫_e^2 ^(+∞) ((2dt)/((1+a)t^2 +(1+a) +2(1−a)t)) let decompose F(t)= (2/((1+a)t^2 +2(1−a)t +1+a)) Δ^′ =(1−a)^2 −(1+a)^2 =1−2a +a^2 −1−2a−a^2 =−4a case 1 −4a>0 ⇒a<0 ⇒t_1 =((−1+a+(√(−4a)))/(1+a)) and t_2 =F((−1+a −(√(−4a)))/(1+a)) (we suppose a≠−1) ⇒ F(t)=(a/(t−t_1 )) +(b/(t−t_2 )) =(2/((1+a)(t−t_1 )(t−t_2 ))) ⇒ a = (2/((1+a)(t_1 −t_2 ))) =(2/((1+a)((2(√(−4a)))/(1+a)))) =(1/( (√(−4a)))) =(1/(2(√(−a)))) b=(2/((1+a)(−2((√(−4a))/(1+a))))) =−(1/( (√(−4a)))) =−(1/(2(√(−a)))) so ∫_e^2 ^(+∞) F(t)dt = (1/(2(√(−a)))){ ∫_e^2 ^(+∞) (dt/(t−t_1 )) −∫_e^2 ^+ (dt/(t−t_2 ))} =(1/(2(√(−a))))[ln∣((t−t_1 )/(t−t_2 ))∣]_e^2 ^(+∞) =(1/(2(√(−a)))){−ln∣((e^2 −t_1 )/(e^2 −t_2 ))∣} =f(a) case2 −4a<0 ⇒4a>0 ⇒Δ^′ <0 ⇒F(t)=(2/((1+a){t^2 +2((1−a)/(1+a))t +1})) = (2/(1+a)) (1/({ t^2 +2 ((1−a)/(1+a))t +(((1−a)/(1+a)))^2 + 1−(((1−a)/(1+a)))^2 })) ⇒ ∫_e^2 ^(+∞) F(t)dt =(2/(1+a)) ∫_e^2 ^(+∞) (dt/({t +((1−a)/(1+a))}^2 +(((1+a)^2 −(1−a)^2 )/((1+a)^2 )))) =(2/(1+a)) ∫_e^2 ^(+∞) (dt/({t+((1−a)/(1+a))}^2 +((4a)/((1+a)^2 )))) =_(t +((1−a)/(1+a))=((2a)/((1+a)))u) (2/(1+a)) ∫_(((1+a)e^2 +1−a)/(2a)) ^(+∞ ) (1/(((4a)/((1+a)^2 ))(1+u^2 )))((2a)/(1+a))du =((4a)/((1+a)^2 )) (((1+a)^2 )/(4a)) ∫_(((1+a)e^2 +1−a)/(2a)) ^(+∞) (du/(1+u^2 )) =(π/2) −arctan((((1+a)e^2 +1−a)/(2a)))=f(a).](https://www.tinkutara.com/question/Q44241.png)
$$\left.\mathrm{1}\right)\:{we}\:{have}\:{f}\left({a}\right)=\:\int_{\mathrm{1}} ^{+\infty} \:\:\:\frac{{dx}}{\frac{\mathrm{1}+{ch}\left(\mathrm{2}{x}\right)}{\mathrm{2}}\:+{a}\:\frac{{ch}\left(\mathrm{2}{x}\right)−\mathrm{1}}{\mathrm{2}}} \\ $$$$=\:\int_{\mathrm{1}} ^{+\infty} \:\:\:\:\frac{\mathrm{2}{dx}}{\mathrm{1}+{ch}\left(\mathrm{2}{x}\right)+{ach}\left(\mathrm{2}{x}\right)−{a}}\:=\:\int_{\mathrm{1}} ^{+\infty} \:\:\:\:\frac{\mathrm{2}{dx}}{\left(\mathrm{1}+{a}\right){ch}\left(\mathrm{2}{x}\right)\:+\mathrm{1}−{a}} \\ $$$$=\:\int_{\mathrm{1}} ^{+\infty} \:\:\:\:\:\:\frac{\mathrm{2}{dx}}{\left(\mathrm{1}+{a}\right)\frac{{e}^{\mathrm{2}{x}} \:+{e}^{−\mathrm{2}{x}} }{\mathrm{2}}\:+\mathrm{1}−{a}}\:=\int_{\mathrm{1}} ^{+\infty} \:\:\frac{\mathrm{4}{dx}}{\left(\mathrm{1}+{a}\right)\left({e}^{\mathrm{2}{x}} \:+{e}^{−\mathrm{2}{x}} \right)\:+\mathrm{2}−\mathrm{2}{a}} \\ $$$$=_{{e}^{\mathrm{2}{x}} ={t}} \:\:\:\int_{{e}^{\mathrm{2}} } ^{+\infty} \:\:\:\:\:\:\:\:\frac{\mathrm{4}}{\left(\mathrm{1}+{a}\right)\left({t}+{t}^{−\mathrm{1}} \right)\:+\mathrm{2}−\mathrm{2}{a}}\:\frac{{dt}}{\mathrm{2}{t}} \\ $$$$=\:\int_{{e}^{\mathrm{2}} } ^{+\infty} \:\:\:\:\:\:\frac{\mathrm{2}{dt}}{\left(\mathrm{1}+{a}\right){t}^{\mathrm{2}} \:+\left(\mathrm{1}+{a}\right)\:+\mathrm{2}\left(\mathrm{1}−{a}\right){t}}\:\:{let}\:{decompose} \\ $$$${F}\left({t}\right)=\:\frac{\mathrm{2}}{\left(\mathrm{1}+{a}\right){t}^{\mathrm{2}} \:+\mathrm{2}\left(\mathrm{1}−{a}\right){t}\:+\mathrm{1}+{a}} \\ $$$$\Delta^{'} \:=\left(\mathrm{1}−{a}\right)^{\mathrm{2}} −\left(\mathrm{1}+{a}\right)^{\mathrm{2}} \:=\mathrm{1}−\mathrm{2}{a}\:+{a}^{\mathrm{2}} \:−\mathrm{1}−\mathrm{2}{a}−{a}^{\mathrm{2}} \:=−\mathrm{4}{a}\: \\ $$$${case}\:\mathrm{1}\:−\mathrm{4}{a}>\mathrm{0}\:\Rightarrow{a}<\mathrm{0}\:\Rightarrow{t}_{\mathrm{1}} =\frac{−\mathrm{1}+{a}+\sqrt{−\mathrm{4}{a}}}{\mathrm{1}+{a}}\:\:{and}\:{t}_{\mathrm{2}} ={F}\frac{−\mathrm{1}+{a}\:−\sqrt{−\mathrm{4}{a}}}{\mathrm{1}+{a}} \\ $$$$\left({we}\:{suppose}\:{a}\neq−\mathrm{1}\right)\:\Rightarrow \\ $$$${F}\left({t}\right)=\frac{{a}}{{t}−{t}_{\mathrm{1}} }\:+\frac{{b}}{{t}−{t}_{\mathrm{2}} }\:=\frac{\mathrm{2}}{\left(\mathrm{1}+{a}\right)\left({t}−{t}_{\mathrm{1}} \right)\left({t}−{t}_{\mathrm{2}} \right)}\:\Rightarrow \\ $$$${a}\:=\:\frac{\mathrm{2}}{\left(\mathrm{1}+{a}\right)\left({t}_{\mathrm{1}} −{t}_{\mathrm{2}} \right)}\:=\frac{\mathrm{2}}{\left(\mathrm{1}+{a}\right)\frac{\mathrm{2}\sqrt{−\mathrm{4}{a}}}{\mathrm{1}+{a}}}\:=\frac{\mathrm{1}}{\:\sqrt{−\mathrm{4}{a}}}\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{−{a}}} \\ $$$${b}=\frac{\mathrm{2}}{\left(\mathrm{1}+{a}\right)\left(−\mathrm{2}\frac{\sqrt{−\mathrm{4}{a}}}{\mathrm{1}+{a}}\right)}\:=−\frac{\mathrm{1}}{\:\sqrt{−\mathrm{4}{a}}}\:=−\frac{\mathrm{1}}{\mathrm{2}\sqrt{−{a}}}\:{so} \\ $$$$\int_{{e}^{\mathrm{2}} } ^{+\infty} \:{F}\left({t}\right){dt}\:=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{−{a}}}\left\{\:\int_{{e}^{\mathrm{2}} } ^{+\infty} \:\frac{{dt}}{{t}−{t}_{\mathrm{1}} }\:−\int_{{e}^{\mathrm{2}} } ^{+} \:\:\frac{{dt}}{{t}−{t}_{\mathrm{2}} }\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{−{a}}}\left[{ln}\mid\frac{{t}−{t}_{\mathrm{1}} }{{t}−{t}_{\mathrm{2}} }\mid\right]_{{e}^{\mathrm{2}} } ^{+\infty} \:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{−{a}}}\left\{−{ln}\mid\frac{{e}^{\mathrm{2}} −{t}_{\mathrm{1}} }{{e}^{\mathrm{2}} −{t}_{\mathrm{2}} }\mid\right\}\:={f}\left({a}\right) \\ $$$${case}\mathrm{2}\:−\mathrm{4}{a}<\mathrm{0}\:\Rightarrow\mathrm{4}{a}>\mathrm{0}\:\Rightarrow\Delta^{'} \:<\mathrm{0}\:\Rightarrow{F}\left({t}\right)=\frac{\mathrm{2}}{\left(\mathrm{1}+{a}\right)\left\{{t}^{\mathrm{2}} \:+\mathrm{2}\frac{\mathrm{1}−{a}}{\mathrm{1}+{a}}{t}\:+\mathrm{1}\right\}} \\ $$$$=\:\frac{\mathrm{2}}{\mathrm{1}+{a}}\:\:\frac{\mathrm{1}}{\left\{\:{t}^{\mathrm{2}} \:+\mathrm{2}\:\frac{\mathrm{1}−\boldsymbol{{a}}}{\mathrm{1}+\boldsymbol{{a}}}\boldsymbol{{t}}\:\:+\left(\frac{\mathrm{1}−\boldsymbol{{a}}}{\mathrm{1}+\boldsymbol{{a}}}\right)^{\mathrm{2}} \:+\:\mathrm{1}−\left(\frac{\mathrm{1}−\boldsymbol{{a}}}{\mathrm{1}+\boldsymbol{{a}}}\right)^{\mathrm{2}} \right\}}\:\Rightarrow \\ $$$$\int_{{e}^{\mathrm{2}} } ^{+\infty} \:\:\:{F}\left({t}\right){dt}\:=\frac{\mathrm{2}}{\mathrm{1}+{a}}\:\int_{{e}^{\mathrm{2}} } ^{+\infty} \:\frac{{dt}}{\left\{{t}\:+\frac{\mathrm{1}−{a}}{\mathrm{1}+{a}}\right\}^{\mathrm{2}} \:+\frac{\left(\mathrm{1}+{a}\right)^{\mathrm{2}} −\left(\mathrm{1}−{a}\right)^{\mathrm{2}} }{\left(\mathrm{1}+{a}\right)^{\mathrm{2}} }} \\ $$$$=\frac{\mathrm{2}}{\mathrm{1}+{a}}\:\int_{{e}^{\mathrm{2}} } ^{+\infty} \:\:\:\:\:\:\:\frac{{dt}}{\left\{{t}+\frac{\mathrm{1}−{a}}{\mathrm{1}+{a}}\right\}^{\mathrm{2}} \:+\frac{\mathrm{4}{a}}{\left(\mathrm{1}+{a}\right)^{\mathrm{2}} }}\:=_{{t}\:+\frac{\mathrm{1}−{a}}{\mathrm{1}+{a}}=\frac{\mathrm{2}{a}}{\left(\mathrm{1}+{a}\right)}{u}} \frac{\mathrm{2}}{\mathrm{1}+{a}}\:\int_{\frac{\left(\mathrm{1}+{a}\right){e}^{\mathrm{2}} \:+\mathrm{1}−{a}}{\mathrm{2}{a}}} ^{+\infty\:\:\:\:\:\:} \:\:\:\frac{\mathrm{1}}{\frac{\mathrm{4}{a}}{\left(\mathrm{1}+{a}\right)^{\mathrm{2}} }\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}\frac{\mathrm{2}{a}}{\mathrm{1}+{a}}{du} \\ $$$$=\frac{\mathrm{4}{a}}{\left(\mathrm{1}+{a}\right)^{\mathrm{2}} }\:\frac{\left(\mathrm{1}+{a}\right)^{\mathrm{2}} }{\mathrm{4}{a}}\:\int_{\frac{\left(\mathrm{1}+{a}\right){e}^{\mathrm{2}} \:+\mathrm{1}−{a}}{\mathrm{2}{a}}} ^{+\infty} \:\:\:\:\frac{{du}}{\mathrm{1}+{u}^{\mathrm{2}} }\:=\frac{\pi}{\mathrm{2}}\:−{arctan}\left(\frac{\left(\mathrm{1}+{a}\right){e}^{\mathrm{2}} \:+\mathrm{1}−{a}}{\mathrm{2}{a}}\right)={f}\left({a}\right). \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 24/Sep/18
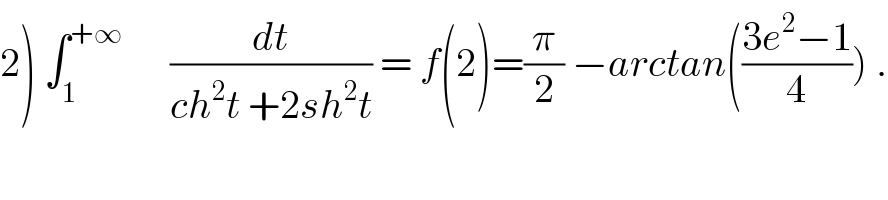
$$\left.\mathrm{2}\right)\:\int_{\mathrm{1}} ^{+\infty} \:\:\:\:\:\:\frac{{dt}}{{ch}^{\mathrm{2}} {t}\:+\mathrm{2}{sh}^{\mathrm{2}} {t}}\:=\:{f}\left(\mathrm{2}\right)=\frac{\pi}{\mathrm{2}}\:−{arctan}\left(\frac{\mathrm{3}{e}^{\mathrm{2}} −\mathrm{1}}{\mathrm{4}}\right)\:. \\ $$
