Menu Close

find-f-x-0-1-arctan-xt-2-dt-

Tinku Tara 0 Comments
Pin




Question Number 41280 by math khazana by abdo last updated on 04/Aug/18
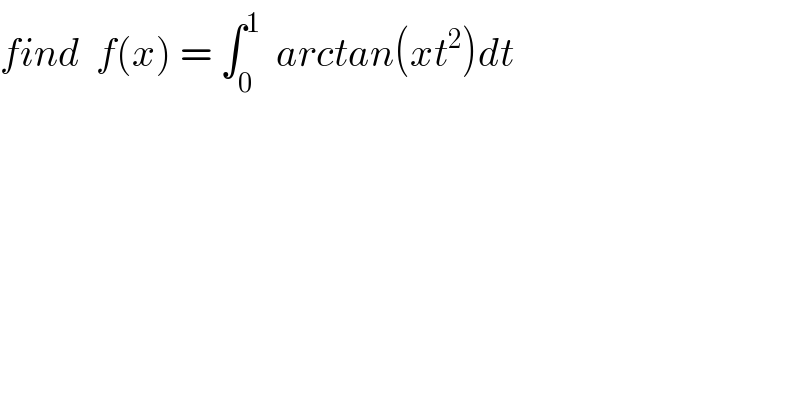
find f(x) = ∫_0 ^1 arctan(xt^2 )dt
$${find}\:\:{f}\left({x}\right)\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{arctan}\left({xt}^{\mathrm{2}} \right){dt} \\ $$
Commented by math khazana by abdo last updated on 07/Aug/18
add ∣x∣<1 to Q.
$${add}\:\mid{x}\mid<\mathrm{1}\:{to}\:{Q}. \\ $$
Answered by math khazana by abdo last updated on 07/Aug/18
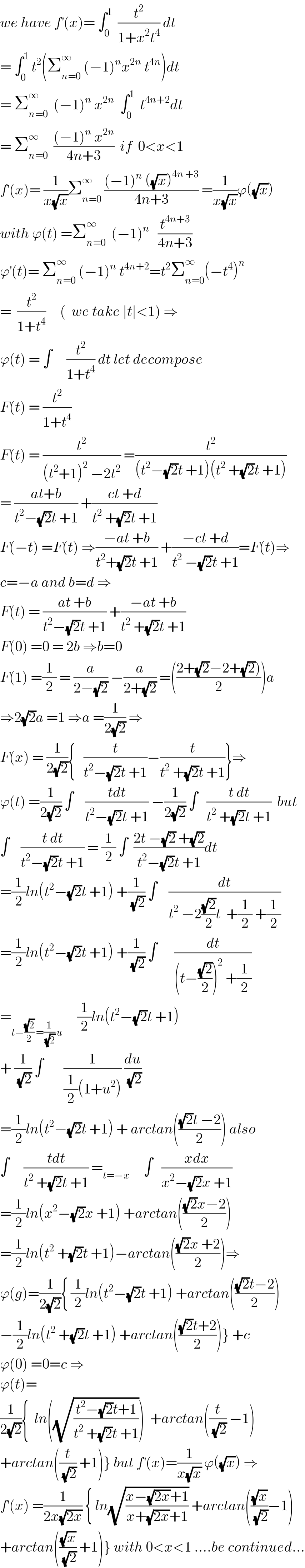
we have f^′ (x)= ∫_0 ^1 (t^2 /(1+x^2 t^4 )) dt = ∫_0 ^1 t^2 (Σ_(n=0) ^∞ (−1)^n x^(2n) t^(4n) )dt = Σ_(n=0) ^∞ (−1)^n x^(2n) ∫_0 ^1 t^(4n+2) dt = Σ_(n=0) ^∞ (((−1)^n x^(2n) )/(4n+3)) if 0<x<1 f^′ (x)= (1/(x(√x)))Σ_(n=0) ^∞ (((−1)^n ((√x))^(4n +3) )/(4n+3)) =(1/(x(√x)))ϕ((√x)) with ϕ(t) =Σ_(n=0) ^∞ (−1)^n (t^(4n+3) /(4n+3)) ϕ^′ (t)= Σ_(n=0) ^∞ (−1)^n t^(4n+2) =t^2 Σ_(n=0) ^∞ (−t^4 )^n = (t^2 /(1+t^4 )) ( we take ∣t∣<1) ⇒ ϕ(t) = ∫ (t^2 /(1+t^4 )) dt let decompose F(t) = (t^2 /(1+t^4 )) F(t) = (t^2 /((t^2 +1)^2 −2t^2 )) =(t^2 /((t^2 −(√2)t +1)(t^2 +(√2)t +1))) = ((at+b)/(t^2 −(√2)t +1)) +((ct +d)/(t^2 +(√2)t +1)) F(−t) =F(t) ⇒((−at +b)/(t^2 +(√2)t +1)) +((−ct +d)/(t^2 −(√2)t +1))=F(t)⇒ c=−a and b=d ⇒ F(t) = ((at +b)/(t^2 −(√2)t +1)) +((−at +b)/(t^2 +(√2)t +1)) F(0) =0 = 2b ⇒b=0 F(1) =(1/2) = (a/(2−(√2))) −(a/(2+(√2))) =(((2+(√2)−2+(√2)))/2))a ⇒2(√2)a =1 ⇒a =(1/(2(√2))) ⇒ F(x) = (1/(2(√2))){ (t/(t^2 −(√2)t +1))−(t/(t^2 +(√2)t +1))}⇒ ϕ(t) =(1/(2(√2))) ∫ ((tdt)/(t^2 −(√2)t +1)) −(1/(2(√2))) ∫ ((t dt)/(t^2 +(√2)t +1)) but ∫ ((t dt)/(t^2 −(√2)t +1)) = (1/2) ∫ ((2t −(√2) +(√2))/(t^2 −(√2)t +1))dt =(1/2)ln(t^2 −(√2)t +1) +(1/( (√2))) ∫ (dt/(t^2 −2((√2)/2)t +(1/2) +(1/2))) =(1/2)ln(t^2 −(√2)t +1) +(1/( (√2))) ∫ (dt/((t−((√2)/2))^2 +(1/2))) =_(t−((√2)/2) =(1/( (√2))) u) (1/2)ln(t^2 −(√2)t +1) + (1/( (√2))) ∫ (1/((1/2)(1+u^2 ))) (du/( (√2))) =(1/2)ln(t^2 −(√2)t +1) + arctan((((√2)t −2)/2)) also ∫ ((tdt)/(t^2 +(√2)t +1)) =_(t=−x) ∫ ((xdx)/(x^2 −(√2)x +1)) =(1/2)ln(x^2 −(√2)x +1) +arctan((((√2)x−2)/2)) =(1/2)ln(t^2 +(√2)t +1)−arctan((((√2)x +2)/2))⇒ ϕ(g)=(1/(2(√2))){ (1/2)ln(t^2 −(√2)t +1) +arctan((((√2)t−2)/2)) −(1/2)ln(t^2 +(√2)t +1) +arctan((((√2)t+2)/2))} +c ϕ(0) =0=c ⇒ ϕ(t)= (1/(2(√2))){ ln((√((t^2 −(√2)t+1)/(t^2 +(√2)t +1)))) +arctan((t/( (√2))) −1) +arctan((t/( (√2))) +1)} but f^′ (x)=(1/(x(√x))) ϕ((√x)) ⇒ f^′ (x) =(1/(2x(√(2x)))) { ln(√((x−(√(2x))+1)/(x+(√(2x))+1))) +arctan(((√x)/( (√2)))−1) +arctan(((√x)/( (√2))) +1)} with 0<x<1 ....be continued...
$${we}\:{have}\:{f}^{'} \left({x}\right)=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{t}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} {t}^{\mathrm{4}} }\:{dt} \\ $$$$=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{t}^{\mathrm{2}} \left(\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} {x}^{\mathrm{2}{n}} \:{t}^{\mathrm{4}{n}} \right){dt} \\ $$$$=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\left(−\mathrm{1}\right)^{{n}} \:{x}^{\mathrm{2}{n}} \:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{t}^{\mathrm{4}{n}+\mathrm{2}} {dt} \\ $$$$=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} \:{x}^{\mathrm{2}{n}} }{\mathrm{4}{n}+\mathrm{3}}\:\:{if}\:\:\mathrm{0}<{x}<\mathrm{1} \\ $$$${f}^{'} \left({x}\right)=\:\frac{\mathrm{1}}{{x}\sqrt{{x}}}\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} \:\left(\sqrt{{x}}\right)^{\mathrm{4}{n}\:+\mathrm{3}} }{\mathrm{4}{n}+\mathrm{3}}\:=\frac{\mathrm{1}}{{x}\sqrt{{x}}}\varphi\left(\sqrt{{x}}\right) \\ $$$${with}\:\varphi\left({t}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\left(−\mathrm{1}\right)^{{n}} \:\:\:\frac{{t}^{\mathrm{4}{n}+\mathrm{3}} }{\mathrm{4}{n}+\mathrm{3}} \\ $$$$\varphi^{'} \left({t}\right)=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} \:{t}^{\mathrm{4}{n}+\mathrm{2}} ={t}^{\mathrm{2}} \sum_{{n}=\mathrm{0}} ^{\infty} \left(−{t}^{\mathrm{4}} \right)^{{n}} \\ $$$$=\:\:\frac{{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{4}} }\:\:\:\:\:\left(\:\:{we}\:{take}\:\mid{t}\mid<\mathrm{1}\right)\:\Rightarrow \\ $$$$\varphi\left({t}\right)\:=\:\int\:\:\:\:\:\frac{{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{4}} }\:{dt}\:{let}\:{decompose} \\ $$$${F}\left({t}\right)\:=\:\frac{{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{4}} } \\ $$$${F}\left({t}\right)\:=\:\frac{{t}^{\mathrm{2}} }{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} \:−\mathrm{2}{t}^{\mathrm{2}} }\:=\frac{{t}^{\mathrm{2}} }{\left({t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}\:+\mathrm{1}\right)\left({t}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}{t}\:+\mathrm{1}\right)} \\ $$$$=\:\frac{{at}+{b}}{{t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}\:+\mathrm{1}}\:+\frac{{ct}\:+{d}}{{t}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}{t}\:+\mathrm{1}}\: \\ $$$${F}\left(−{t}\right)\:={F}\left({t}\right)\:\Rightarrow\frac{−{at}\:+{b}}{{t}^{\mathrm{2}} +\sqrt{\mathrm{2}}{t}\:+\mathrm{1}}\:+\frac{−{ct}\:+{d}}{{t}^{\mathrm{2}} \:−\sqrt{\mathrm{2}}{t}\:+\mathrm{1}}={F}\left({t}\right)\Rightarrow \\ $$$${c}=−{a}\:{and}\:{b}={d}\:\Rightarrow \\ $$$${F}\left({t}\right)\:=\:\frac{{at}\:+{b}}{{t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}\:+\mathrm{1}}\:+\frac{−{at}\:+{b}}{{t}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}{t}\:+\mathrm{1}} \\ $$$${F}\left(\mathrm{0}\right)\:=\mathrm{0}\:=\:\mathrm{2}{b}\:\Rightarrow{b}=\mathrm{0} \\ $$$${F}\left(\mathrm{1}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\:=\:\frac{{a}}{\mathrm{2}−\sqrt{\mathrm{2}}}\:−\frac{{a}}{\mathrm{2}+\sqrt{\mathrm{2}}}\:=\left(\frac{\left.\mathrm{2}+\sqrt{\mathrm{2}}−\mathrm{2}+\sqrt{\mathrm{2}}\right)}{\mathrm{2}}\right){a} \\ $$$$\Rightarrow\mathrm{2}\sqrt{\mathrm{2}}{a}\:=\mathrm{1}\:\Rightarrow{a}\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\Rightarrow \\ $$$${F}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\left\{\:\:\:\frac{{t}}{{t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}\:+\mathrm{1}}−\frac{{t}}{{t}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}{t}\:+\mathrm{1}}\right\}\Rightarrow \\ $$$$\varphi\left({t}\right)\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\int\:\:\:\:\frac{{tdt}}{{t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}\:+\mathrm{1}}\:−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\int\:\:\:\frac{{t}\:{dt}}{{t}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}{t}\:+\mathrm{1}}\:\:{but} \\ $$$$\int\:\:\:\:\frac{{t}\:{dt}}{{t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}\:+\mathrm{1}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\:\frac{\mathrm{2}{t}\:−\sqrt{\mathrm{2}}\:+\sqrt{\mathrm{2}}}{{t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}\:+\mathrm{1}}{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}\:+\mathrm{1}\right)\:+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\int\:\:\:\:\frac{{dt}}{{t}^{\mathrm{2}} \:−\mathrm{2}\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}{t}\:\:+\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}\:+\mathrm{1}\right)\:+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\int\:\:\:\:\:\:\frac{{dt}}{\left({t}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$=_{{t}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:{u}} \:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}\:+\mathrm{1}\right) \\ $$$$+\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\int\:\:\:\:\:\:\:\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}\:\frac{{du}}{\:\sqrt{\mathrm{2}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}\:+\mathrm{1}\right)\:+\:{arctan}\left(\frac{\sqrt{\mathrm{2}}{t}\:−\mathrm{2}}{\mathrm{2}}\right)\:{also} \\ $$$$\int\:\:\:\:\:\frac{{tdt}}{{t}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}{t}\:+\mathrm{1}}\:=_{{t}=−{x}} \:\:\:\:\:\int\:\:\:\frac{{xdx}}{{x}^{\mathrm{2}} −\sqrt{\mathrm{2}}{x}\:+\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({x}^{\mathrm{2}} −\sqrt{\mathrm{2}}{x}\:+\mathrm{1}\right)\:+{arctan}\left(\frac{\sqrt{\mathrm{2}}{x}−\mathrm{2}}{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({t}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}{t}\:+\mathrm{1}\right)−{arctan}\left(\frac{\sqrt{\mathrm{2}}{x}\:+\mathrm{2}}{\mathrm{2}}\right)\Rightarrow \\ $$$$\varphi\left({g}\right)=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\left\{\:\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}\:+\mathrm{1}\right)\:+{arctan}\left(\frac{\sqrt{\mathrm{2}}{t}−\mathrm{2}}{\mathrm{2}}\right)\right. \\ $$$$\left.−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({t}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}{t}\:+\mathrm{1}\right)\:+{arctan}\left(\frac{\sqrt{\mathrm{2}}{t}+\mathrm{2}}{\mathrm{2}}\right)\right\}\:+{c} \\ $$$$\varphi\left(\mathrm{0}\right)\:=\mathrm{0}={c}\:\Rightarrow \\ $$$$\varphi\left({t}\right)= \\ $$$$\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\left\{\:\:{ln}\left(\sqrt{\frac{{t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}+\mathrm{1}}{{t}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}{t}\:+\mathrm{1}}}\right)\:\:+{arctan}\left(\frac{{t}}{\:\sqrt{\mathrm{2}}}\:−\mathrm{1}\right)\right. \\ $$$$\left.+{arctan}\left(\frac{{t}}{\:\sqrt{\mathrm{2}}}\:+\mathrm{1}\right)\right\}\:{but}\:{f}^{'} \left({x}\right)=\frac{\mathrm{1}}{{x}\sqrt{{x}}}\:\varphi\left(\sqrt{{x}}\right)\:\Rightarrow \\ $$$${f}^{'} \left({x}\right)\:=\frac{\mathrm{1}}{\mathrm{2}{x}\sqrt{\mathrm{2}{x}}}\:\left\{\:{ln}\sqrt{\frac{{x}−\sqrt{\mathrm{2}{x}}+\mathrm{1}}{{x}+\sqrt{\mathrm{2}{x}}+\mathrm{1}}}\:+{arctan}\left(\frac{\sqrt{{x}}}{\:\sqrt{\mathrm{2}}}−\mathrm{1}\right)\right. \\ $$$$\left.+{arctan}\left(\frac{\sqrt{{x}}}{\:\sqrt{\mathrm{2}}}\:+\mathrm{1}\right)\right\}\:{with}\:\mathrm{0}<{x}<\mathrm{1}\:….{be}\:{continued}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *