Menu Close

find-f-x-0-1-ln-1-xt-2-dt-with-x-gt-0-2-give-thevalue-of-0-1-ln-1-t-2-dt-and-0-1-ln-1-2t-2-dt-

Tinku Tara 0 Comments
Pin




Question Number 31502 by abdo imad last updated on 09/Mar/18
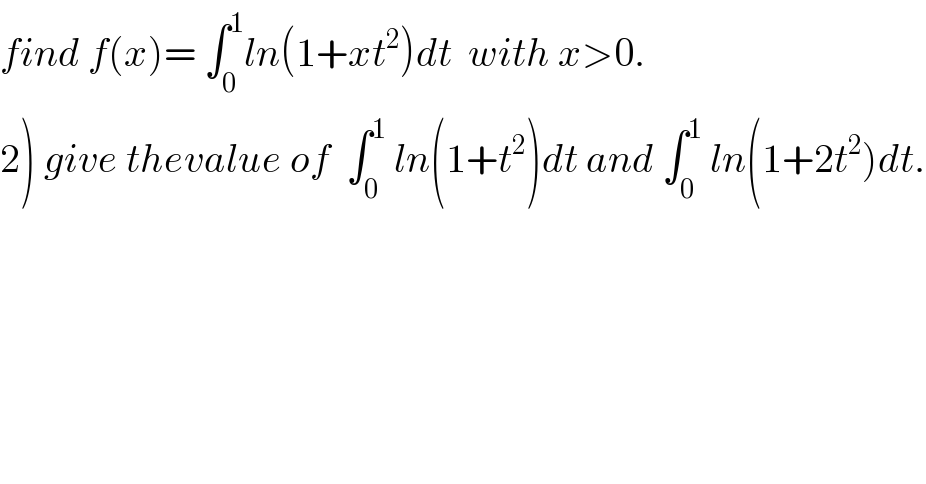
find f(x)= ∫_0 ^1 ln(1+xt^2 )dt with x>0. 2) give thevalue of ∫_0 ^1 ln(1+t^2 )dt and ∫_0 ^1 ln(1+2t^2 )dt.
$${find}\:{f}\left({x}\right)=\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{xt}^{\mathrm{2}} \right){dt}\:\:{with}\:{x}>\mathrm{0}. \\ $$$$\left.\mathrm{2}\right)\:{give}\:{thevalue}\:{of}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right){dt}\:{and}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{ln}\left(\mathrm{1}+\mathrm{2}{t}^{\mathrm{2}} \right){dt}. \\ $$
Commented by abdo imad last updated on 15/Mar/18
we have f^′ (x)= ∫_0 ^1 (t^2 /(1+xt^2 ))dt =(1/x) ∫_0 ^1 ((xt^2 )/(1+xt^2 ))dt =(1/x) ∫_0 ^1 ((1+xt^2 −1)/(1+xt^2 ))dt = (1/x) −(1/x) ∫_0 ^1 (dt/(1+xt^2 )) ch.(√x) t=u give ∫_0 ^1 (dt/(1+xt^2 )) = ∫_0 ^((√x) ) (1/(1+u^2 )) (du/( (√x) )) =(1/( (√x) )) ∫_0 ^(√x) (du/(1+u^2 )) = (1/( (√x))) artan((√x)) ⇒ f^′ (x)= (1/x) −((arctan((√(x))))/(x(√x) )) ⇒ f(x)=ln∣x∣ −∫_1 ^x ((arctan((√t)))/(t(√t))) dt +λ λ=f(1)=∫_0 ^1 ln(1+t^2 )dt so f(x)=ln(x) −∫_1 ^x ((arctan((√(t))))/(t(√t))) dt +∫_0 ^1 ln(1+t^2 )dt ch.(√t)=u give ∫_1 ^x ((arctan((√t)))/(t(√t)))dt= ∫_1 ^(√x) ((arctanu)/u^3 ) (2u)du =2 ∫_1 ^(√x) ((arctanu)/u^2 )du =2( [−(1/u)arctanu]_1 ^(√x) +∫_1 ^(√x) (du/(u(1+u^2 )))) =2((π/4) −((arctan((√x)))/( (√x))))+2 ∫_1 ^(√x) (du/(u(1+u^2 ))) but ∫_1 ^(√x) (du/(u(1+u^2 ))) =∫_1 ^(√x) ((1/u) −(u/(1+u^2 )))du =[ln(u)−(1/2)ln(1+u^2 )]_1 ^(√x) =[ ln( (u/( (√(1+u^2 )))))]_1 ^(√x) =ln(((√x)/( (√(1+x))))) −ln((1/( (√2))))=ln( ((√x)/( (√(1+x))))) +ln((√(2))) finally f(x)= ln(x)−(π/2) + ((arctan((√x)))/(2(√x))) −2ln(((√x)/( (√(1+x))))) −ln(2) +∫_0 ^1 ln(1+t^2 )dt .
$${we}\:{have}\:{f}^{'} \left({x}\right)=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{t}^{\mathrm{2}} }{\mathrm{1}+{xt}^{\mathrm{2}} }{dt}\:=\frac{\mathrm{1}}{{x}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{xt}^{\mathrm{2}} }{\mathrm{1}+{xt}^{\mathrm{2}} }{dt} \\ $$$$=\frac{\mathrm{1}}{{x}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{1}+{xt}^{\mathrm{2}} \:−\mathrm{1}}{\mathrm{1}+{xt}^{\mathrm{2}} }{dt}\:=\:\frac{\mathrm{1}}{{x}}\:−\frac{\mathrm{1}}{{x}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{dt}}{\mathrm{1}+{xt}^{\mathrm{2}} }\:\:{ch}.\sqrt{{x}}\:{t}={u}\:{give} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{dt}}{\mathrm{1}+{xt}^{\mathrm{2}} }\:=\:\int_{\mathrm{0}} ^{\sqrt{{x}}\:} \:\:\frac{\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{2}} }\:\frac{{du}}{\:\sqrt{{x}}\:}\:=\frac{\mathrm{1}}{\:\sqrt{{x}}\:}\:\int_{\mathrm{0}} ^{\sqrt{{x}}} \:\:\frac{{du}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$$=\:\frac{\mathrm{1}}{\:\sqrt{{x}}}\:{artan}\left(\sqrt{{x}}\right)\:\Rightarrow\:{f}^{'} \left({x}\right)=\:\frac{\mathrm{1}}{{x}}\:−\frac{{arctan}\left(\sqrt{\left.{x}\right)}\right.}{{x}\sqrt{{x}}\:}\:\Rightarrow \\ $$$${f}\left({x}\right)={ln}\mid{x}\mid\:−\int_{\mathrm{1}} ^{{x}} \:\:\:\:\:\frac{{arctan}\left(\sqrt{{t}}\right)}{{t}\sqrt{{t}}}\:{dt}\:+\lambda \\ $$$$\lambda={f}\left(\mathrm{1}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right){dt}\:\:{so} \\ $$$${f}\left({x}\right)={ln}\left({x}\right)\:−\int_{\mathrm{1}} ^{{x}} \:\:\:\frac{{arctan}\left(\sqrt{\left.{t}\right)}\right.}{{t}\sqrt{{t}}}\:{dt}\:\:+\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right){dt}\:{ch}.\sqrt{{t}}={u} \\ $$$${give}\:\int_{\mathrm{1}} ^{{x}} \:\:\frac{{arctan}\left(\sqrt{{t}}\right)}{{t}\sqrt{{t}}}{dt}=\:\int_{\mathrm{1}} ^{\sqrt{{x}}} \:\:\frac{{arctanu}}{{u}^{\mathrm{3}} }\:\left(\mathrm{2}{u}\right){du} \\ $$$$=\mathrm{2}\:\int_{\mathrm{1}} ^{\sqrt{{x}}} \:\:\:\:\frac{{arctanu}}{{u}^{\mathrm{2}} }{du} \\ $$$$=\mathrm{2}\left(\:\left[−\frac{\mathrm{1}}{{u}}{arctanu}\right]_{\mathrm{1}} ^{\sqrt{{x}}} \:+\int_{\mathrm{1}} ^{\sqrt{{x}}} \:\:\:\:\frac{{du}}{{u}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}\right) \\ $$$$=\mathrm{2}\left(\frac{\pi}{\mathrm{4}}\:−\frac{{arctan}\left(\sqrt{{x}}\right)}{\:\sqrt{{x}}}\right)+\mathrm{2}\:\int_{\mathrm{1}} ^{\sqrt{{x}}} \:\:\frac{{du}}{{u}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}\:{but} \\ $$$$\int_{\mathrm{1}} ^{\sqrt{{x}}} \:\:\frac{{du}}{{u}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}\:=\int_{\mathrm{1}} ^{\sqrt{{x}}} \:\left(\frac{\mathrm{1}}{{u}}\:−\frac{{u}}{\mathrm{1}+{u}^{\mathrm{2}} }\right){du} \\ $$$$=\left[{ln}\left({u}\right)−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\right]_{\mathrm{1}} ^{\sqrt{{x}}} =\left[\:{ln}\left(\:\frac{{u}}{\:\sqrt{\mathrm{1}+{u}^{\mathrm{2}} }}\right)\right]_{\mathrm{1}} ^{\sqrt{{x}}} \\ $$$$={ln}\left(\frac{\sqrt{{x}}}{\:\sqrt{\mathrm{1}+{x}}}\right)\:−{ln}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)={ln}\left(\:\frac{\sqrt{{x}}}{\:\sqrt{\mathrm{1}+{x}}}\right)\:+{ln}\left(\sqrt{\left.\mathrm{2}\right)}\:\:\:{finally}\right. \\ $$$${f}\left({x}\right)=\:{ln}\left({x}\right)−\frac{\pi}{\mathrm{2}}\:+\:\frac{{arctan}\left(\sqrt{{x}}\right)}{\mathrm{2}\sqrt{{x}}}\:−\mathrm{2}{ln}\left(\frac{\sqrt{{x}}}{\:\sqrt{\mathrm{1}+{x}}}\right)\:−{ln}\left(\mathrm{2}\right) \\ $$$$+\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right){dt}\:\:. \\ $$$$ \\ $$
Commented by abdo imad last updated on 15/Mar/18
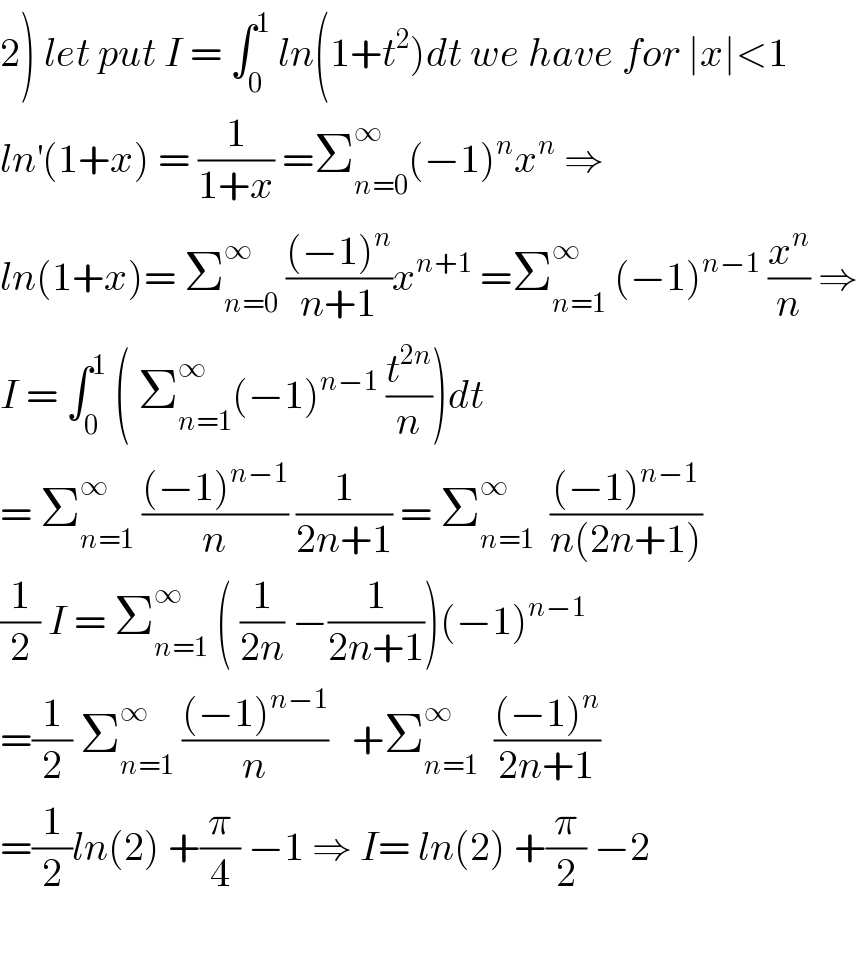
2) let put I = ∫_0 ^1 ln(1+t^2 )dt we have for ∣x∣<1 ln^′ (1+x) = (1/(1+x)) =Σ_(n=0) ^∞ (−1)^n x^n ⇒ ln(1+x)= Σ_(n=0) ^∞ (((−1)^n )/(n+1))x^(n+1) =Σ_(n=1) ^∞ (−1)^(n−1) (x^n /n) ⇒ I = ∫_0 ^1 ( Σ_(n=1) ^∞ (−1)^(n−1) (t^(2n) /n))dt = Σ_(n=1) ^∞ (((−1)^(n−1) )/n) (1/(2n+1)) = Σ_(n=1) ^∞ (((−1)^(n−1) )/(n(2n+1))) (1/2) I = Σ_(n=1) ^∞ ( (1/(2n)) −(1/(2n+1)))(−1)^(n−1) =(1/2) Σ_(n=1) ^∞ (((−1)^(n−1) )/n) +Σ_(n=1) ^∞ (((−1)^n )/(2n+1)) =(1/2)ln(2) +(π/4) −1 ⇒ I= ln(2) +(π/2) −2
$$\left.\mathrm{2}\right)\:{let}\:{put}\:{I}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right){dt}\:{we}\:{have}\:{for}\:\mid{x}\mid<\mathrm{1} \\ $$$${ln}^{'} \left(\mathrm{1}+{x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{1}+{x}}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} {x}^{{n}} \:\Rightarrow \\ $$$${ln}\left(\mathrm{1}+{x}\right)=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}+\mathrm{1}}{x}^{{n}+\mathrm{1}} \:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \:\frac{{x}^{{n}} }{{n}}\:\Rightarrow \\ $$$${I}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\left(\:\sum_{{n}=\mathrm{1}} ^{\infty} \left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \:\frac{{t}^{\mathrm{2}{n}} }{{n}}\right){dt} \\ $$$$=\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\:\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\:=\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}\left(\mathrm{2}{n}+\mathrm{1}\right)} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\:{I}\:=\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\left(\:\frac{\mathrm{1}}{\mathrm{2}{n}}\:−\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\right)\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\:\:\:+\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{2}\right)\:+\frac{\pi}{\mathrm{4}}\:−\mathrm{1}\:\Rightarrow\:{I}=\:{ln}\left(\mathrm{2}\right)\:+\frac{\pi}{\mathrm{2}}\:−\mathrm{2} \\ $$$$ \\ $$
Commented by abdo imad last updated on 15/Mar/18
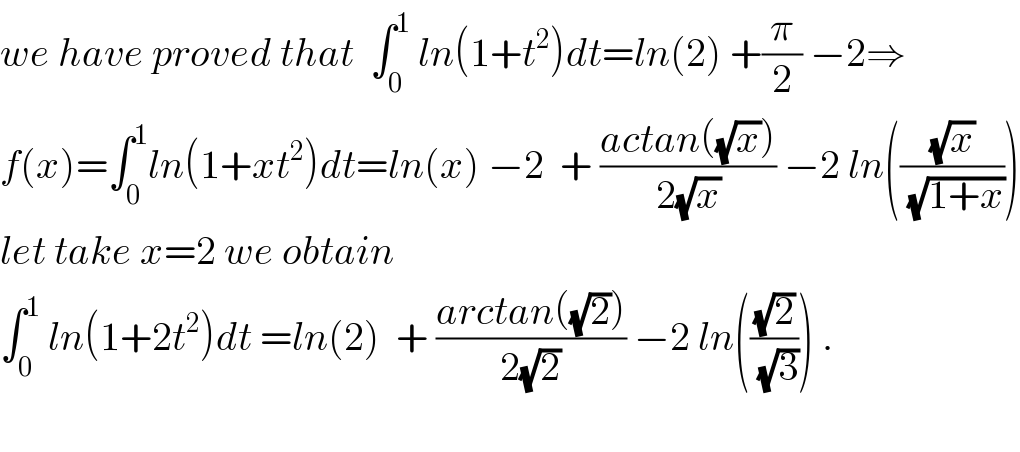
we have proved that ∫_0 ^1 ln(1+t^2 )dt=ln(2) +(π/2) −2⇒ f(x)=∫_0 ^1 ln(1+xt^2 )dt=ln(x) −2 + ((actan((√x)))/(2(√x))) −2 ln(((√x)/( (√(1+x))))) let take x=2 we obtain ∫_0 ^1 ln(1+2t^2 )dt =ln(2) + ((arctan((√2)))/(2(√2))) −2 ln(((√2)/( (√3)))) .
$${we}\:{have}\:{proved}\:{that}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right){dt}={ln}\left(\mathrm{2}\right)\:+\frac{\pi}{\mathrm{2}}\:−\mathrm{2}\Rightarrow \\ $$$${f}\left({x}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{xt}^{\mathrm{2}} \right){dt}={ln}\left({x}\right)\:−\mathrm{2}\:\:+\:\frac{{actan}\left(\sqrt{{x}}\right)}{\mathrm{2}\sqrt{{x}}}\:−\mathrm{2}\:{ln}\left(\frac{\sqrt{{x}}}{\:\sqrt{\mathrm{1}+{x}}}\right) \\ $$$${let}\:{take}\:{x}=\mathrm{2}\:{we}\:{obtain} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:{ln}\left(\mathrm{1}+\mathrm{2}{t}^{\mathrm{2}} \right){dt}\:={ln}\left(\mathrm{2}\right)\:\:+\:\frac{{arctan}\left(\sqrt{\mathrm{2}}\right)}{\mathrm{2}\sqrt{\mathrm{2}}}\:−\mathrm{2}\:{ln}\left(\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{3}}}\right)\:. \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *