Question Number 38461 by maxmathsup by imad last updated on 25/Jun/18
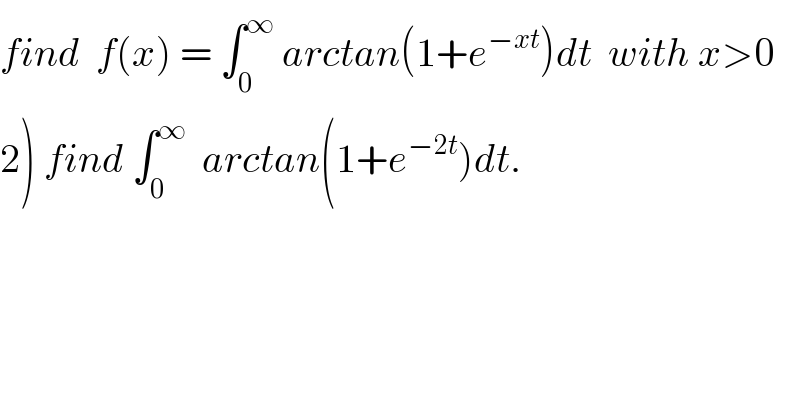
$${find}\:\:{f}\left({x}\right)\:=\:\int_{\mathrm{0}} ^{\infty} \:{arctan}\left(\mathrm{1}+{e}^{−{xt}} \right){dt}\:\:{with}\:{x}>\mathrm{0} \\ $$$$\left.\mathrm{2}\right)\:{find}\:\int_{\mathrm{0}} ^{\infty} \:\:{arctan}\left(\mathrm{1}+{e}^{−\mathrm{2}{t}} \right){dt}. \\ $$
