Menu Close

find-f-x-0-t-arctan-xt-1-t-4-dt-

Tinku Tara 0 Comments
Pin




Question Number 49968 by maxmathsup by imad last updated on 12/Dec/18
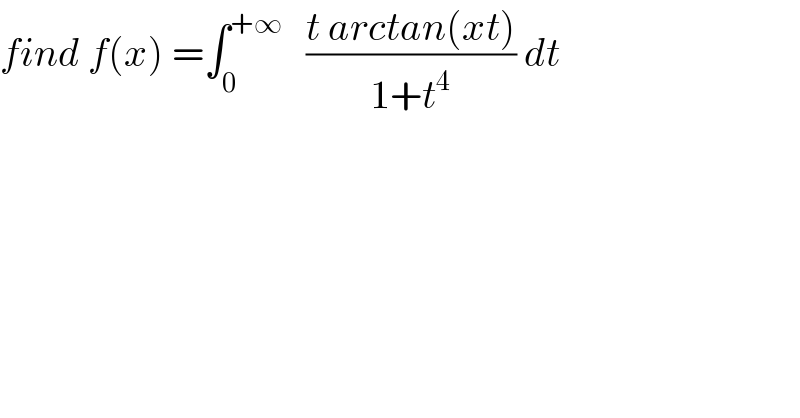
find f(x) =∫_0 ^(+∞) ((t arctan(xt))/(1+t^4 )) dt
$${find}\:{f}\left({x}\right)\:=\int_{\mathrm{0}} ^{+\infty} \:\:\:\frac{{t}\:{arctan}\left({xt}\right)}{\mathrm{1}+{t}^{\mathrm{4}} }\:{dt} \\ $$
Commented by mathmax by abdo last updated on 03/Nov/19
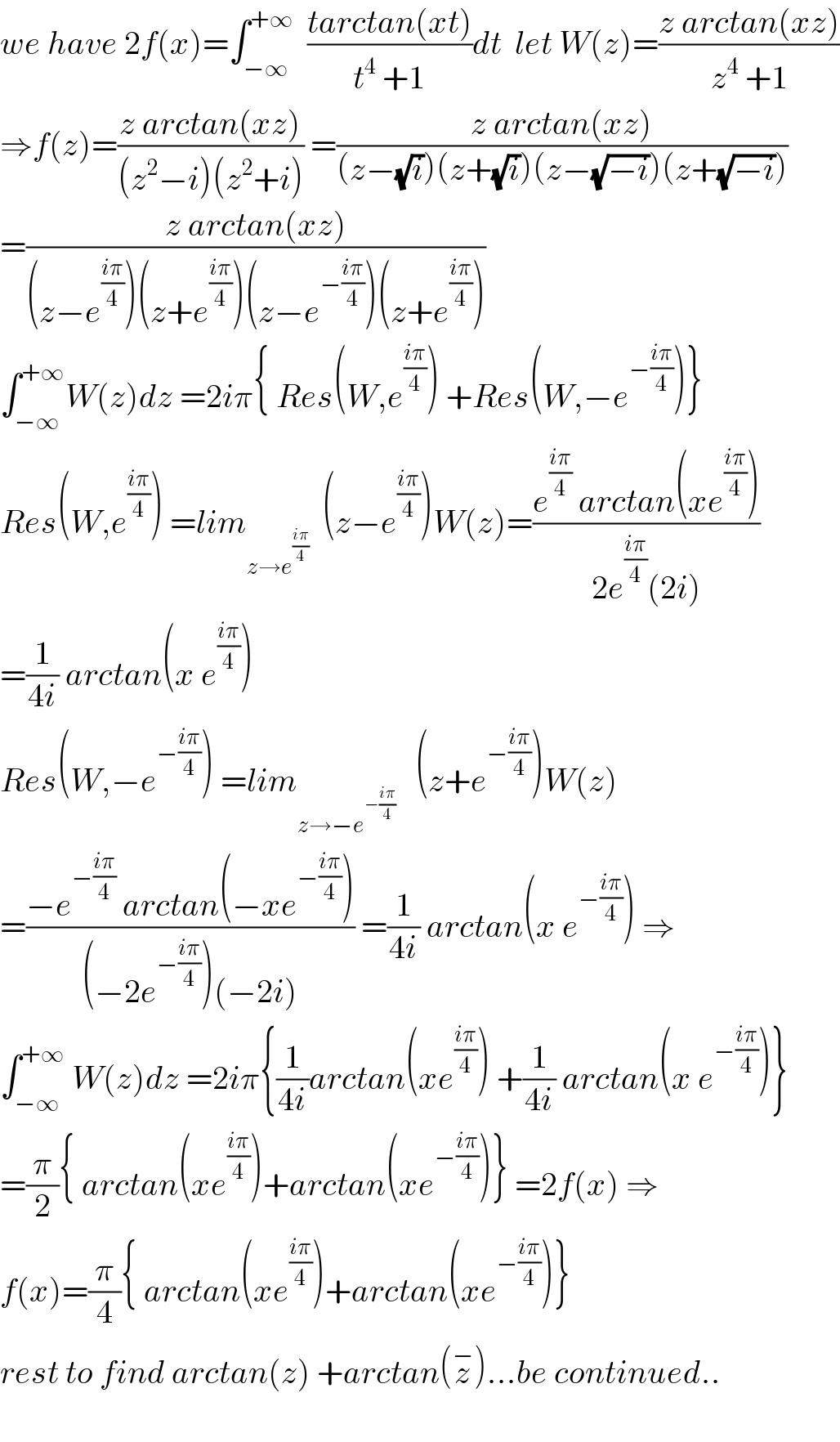
we have 2f(x)=∫_(−∞) ^(+∞) ((tarctan(xt))/(t^4 +1))dt let W(z)=((z arctan(xz))/(z^4 +1)) ⇒f(z)=((z arctan(xz))/((z^2 −i)(z^2 +i))) =((z arctan(xz))/((z−(√i))(z+(√i))(z−(√(−i)))(z+(√(−i))))) =((z arctan(xz))/((z−e^((iπ)/4) )(z+e^((iπ)/4) )(z−e^(−((iπ)/4)) )(z+e^((iπ)/4) ))) ∫_(−∞) ^(+∞) W(z)dz =2iπ{ Res(W,e^((iπ)/4) ) +Res(W,−e^(−((iπ)/4)) )} Res(W,e^((iπ)/4) ) =lim_(z→e^((iπ)/4) ) (z−e^((iπ)/4) )W(z)=((e^((iπ)/4) arctan(xe^((iπ)/4) ))/(2e^((iπ)/4) (2i))) =(1/(4i)) arctan(x e^((iπ)/4) ) Res(W,−e^(−((iπ)/4)) ) =lim_(z→−e^(−((iπ)/4)) ) (z+e^(−((iπ)/4)) )W(z) =((−e^(−((iπ)/4)) arctan(−xe^(−((iπ)/4)) ))/((−2e^(−((iπ)/4)) )(−2i))) =(1/(4i)) arctan(x e^(−((iπ)/4)) ) ⇒ ∫_(−∞) ^(+∞) W(z)dz =2iπ{(1/(4i))arctan(xe^((iπ)/4) ) +(1/(4i)) arctan(x e^(−((iπ)/4)) )} =(π/2){ arctan(xe^((iπ)/4) )+arctan(xe^(−((iπ)/4)) )} =2f(x) ⇒ f(x)=(π/4){ arctan(xe^((iπ)/4) )+arctan(xe^(−((iπ)/4)) )} rest to find arctan(z) +arctan(z^− )...be continued..
$${we}\:{have}\:\mathrm{2}{f}\left({x}\right)=\int_{−\infty} ^{+\infty} \:\:\frac{{tarctan}\left({xt}\right)}{{t}^{\mathrm{4}} \:+\mathrm{1}}{dt}\:\:{let}\:{W}\left({z}\right)=\frac{{z}\:{arctan}\left({xz}\right)}{{z}^{\mathrm{4}} \:+\mathrm{1}} \\ $$$$\Rightarrow{f}\left({z}\right)=\frac{{z}\:{arctan}\left({xz}\right)}{\left({z}^{\mathrm{2}} −{i}\right)\left({z}^{\mathrm{2}} +{i}\right)}\:=\frac{{z}\:{arctan}\left({xz}\right)}{\left({z}−\sqrt{{i}}\right)\left({z}+\sqrt{{i}}\right)\left({z}−\sqrt{−{i}}\right)\left({z}+\sqrt{−{i}}\right)} \\ $$$$=\frac{{z}\:{arctan}\left({xz}\right)}{\left({z}−{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\left({z}+{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\left({z}−{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\left({z}+{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)} \\ $$$$\int_{−\infty} ^{+\infty} {W}\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{\:{Res}\left({W},{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\:+{Res}\left({W},−{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\right\} \\ $$$${Res}\left({W},{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\:={lim}_{{z}\rightarrow{e}^{\frac{{i}\pi}{\mathrm{4}}} } \:\:\left({z}−{e}^{\frac{{i}\pi}{\mathrm{4}}} \right){W}\left({z}\right)=\frac{{e}^{\frac{{i}\pi}{\mathrm{4}}} \:{arctan}\left({xe}^{\frac{{i}\pi}{\mathrm{4}}} \right)}{\mathrm{2}{e}^{\frac{{i}\pi}{\mathrm{4}}} \left(\mathrm{2}{i}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}{i}}\:{arctan}\left({x}\:{e}^{\frac{{i}\pi}{\mathrm{4}}} \right) \\ $$$${Res}\left({W},−{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\:={lim}_{{z}\rightarrow−{e}^{−\frac{{i}\pi}{\mathrm{4}}} } \:\:\:\left({z}+{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right){W}\left({z}\right) \\ $$$$=\frac{−{e}^{−\frac{{i}\pi}{\mathrm{4}}} \:{arctan}\left(−{xe}^{−\frac{{i}\pi}{\mathrm{4}}} \right)}{\left(−\mathrm{2}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\left(−\mathrm{2}{i}\right)}\:=\frac{\mathrm{1}}{\mathrm{4}{i}}\:{arctan}\left({x}\:{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:{W}\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{\frac{\mathrm{1}}{\mathrm{4}{i}}{arctan}\left({xe}^{\frac{{i}\pi}{\mathrm{4}}} \right)\:+\frac{\mathrm{1}}{\mathrm{4}{i}}\:{arctan}\left({x}\:{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\right\} \\ $$$$=\frac{\pi}{\mathrm{2}}\left\{\:{arctan}\left({xe}^{\frac{{i}\pi}{\mathrm{4}}} \right)+{arctan}\left({xe}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\right\}\:=\mathrm{2}{f}\left({x}\right)\:\Rightarrow \\ $$$${f}\left({x}\right)=\frac{\pi}{\mathrm{4}}\left\{\:{arctan}\left({xe}^{\frac{{i}\pi}{\mathrm{4}}} \right)+{arctan}\left({xe}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\right\} \\ $$$${rest}\:{to}\:{find}\:{arctan}\left({z}\right)\:+{arctan}\left(\overset{−} {{z}}\right)…{be}\:{continued}.. \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *