Question Number 36422 by abdo.msup.com last updated on 01/Jun/18
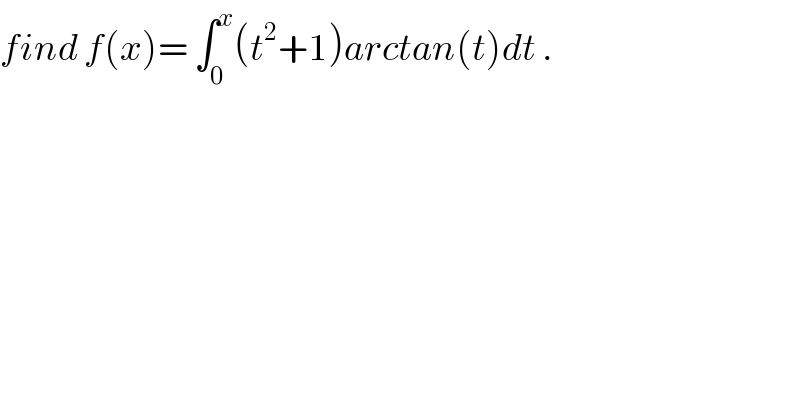
$${find}\:{f}\left({x}\right)=\:\int_{\mathrm{0}} ^{{x}} \left({t}^{\mathrm{2}} +\mathrm{1}\right){arctan}\left({t}\right){dt}\:. \\ $$
Commented by prof Abdo imad last updated on 04/Jun/18
![let integrate by parts u^′ = t^2 +1 and v=arctant f(x) = [ ((t^3 /3) +t)arctan(t)]_0 ^x −∫_0 ^x ((t^3 /3) +t) (dt/(1+t^2 )) =((x^3 /3) +x)arctan(x) −(1/3) ∫_0 ^x ((t^3 +3t)/(1+t^2 )) dt but ∫_0 ^x ((t^3 +3t)/(t^2 +1)) dt =∫_0 ^x ((t(t^2 +1) +2t)/(t^2 +1))dt =∫_0 ^x tdt + ∫_0 ^x ((2t)/(t^2 +1))dt =(x^2 /2) +ln(x^2 +1) so f(x)= ((x^3 /3) +x)arctan(x) −(x^2 /6) −(1/3)ln(1+x^2 ) .](https://www.tinkutara.com/question/Q36681.png)
$${let}\:{integrate}\:{by}\:{parts}\:{u}^{'} =\:{t}^{\mathrm{2}} \:+\mathrm{1}\:{and}\:{v}={arctant} \\ $$$${f}\left({x}\right)\:=\:\left[\:\left(\frac{{t}^{\mathrm{3}} }{\mathrm{3}}\:+{t}\right){arctan}\left({t}\right)\right]_{\mathrm{0}} ^{{x}} \:−\int_{\mathrm{0}} ^{{x}} \:\left(\frac{{t}^{\mathrm{3}} }{\mathrm{3}}\:+{t}\right)\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$=\left(\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\:+{x}\right){arctan}\left({x}\right)\:−\frac{\mathrm{1}}{\mathrm{3}}\:\int_{\mathrm{0}} ^{{x}} \:\:\:\frac{{t}^{\mathrm{3}} \:+\mathrm{3}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\:{dt}\:{but} \\ $$$$\int_{\mathrm{0}} ^{{x}} \:\:\frac{{t}^{\mathrm{3}} \:+\mathrm{3}{t}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:{dt}\:=\int_{\mathrm{0}} ^{{x}} \:\:\frac{{t}\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)\:+\mathrm{2}{t}}{{t}^{\mathrm{2}} \:+\mathrm{1}}{dt} \\ $$$$=\int_{\mathrm{0}} ^{{x}} \:{tdt}\:+\:\int_{\mathrm{0}} ^{{x}} \:\:\:\frac{\mathrm{2}{t}}{{t}^{\mathrm{2}} \:+\mathrm{1}}{dt} \\ $$$$=\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:+{ln}\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)\:\:{so} \\ $$$${f}\left({x}\right)=\:\left(\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\:+{x}\right){arctan}\left({x}\right)\:−\frac{{x}^{\mathrm{2}} }{\mathrm{6}}\:−\frac{\mathrm{1}}{\mathrm{3}}{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\:. \\ $$$$ \\ $$
