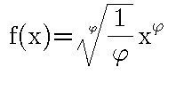Question Number 93786 by mr W last updated on 14/May/20
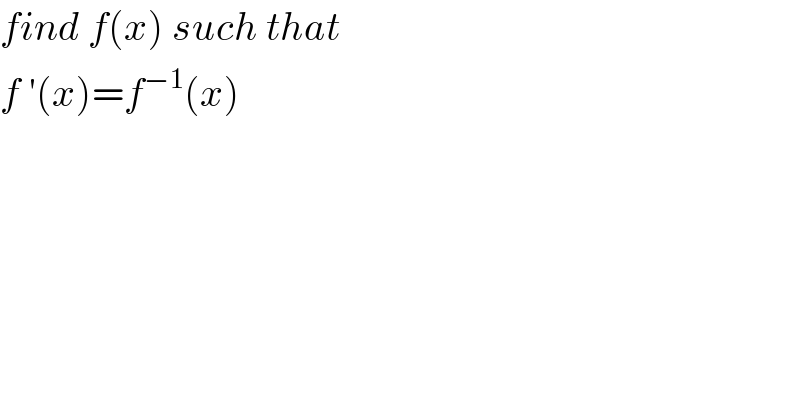
$${find}\:{f}\left({x}\right)\:{such}\:{that} \\ $$$${f}\:'\left({x}\right)={f}^{−\mathrm{1}} \left({x}\right) \\ $$
Answered by john santu last updated on 15/May/20

$$\mathrm{f}\left(\mathrm{x}\right)=\:\sqrt[{\varphi}]{\frac{\mathrm{1}}{\varphi}}\:\mathrm{x}^{\varphi} \: \\ $$
Answered by M±th+et+s last updated on 15/May/20
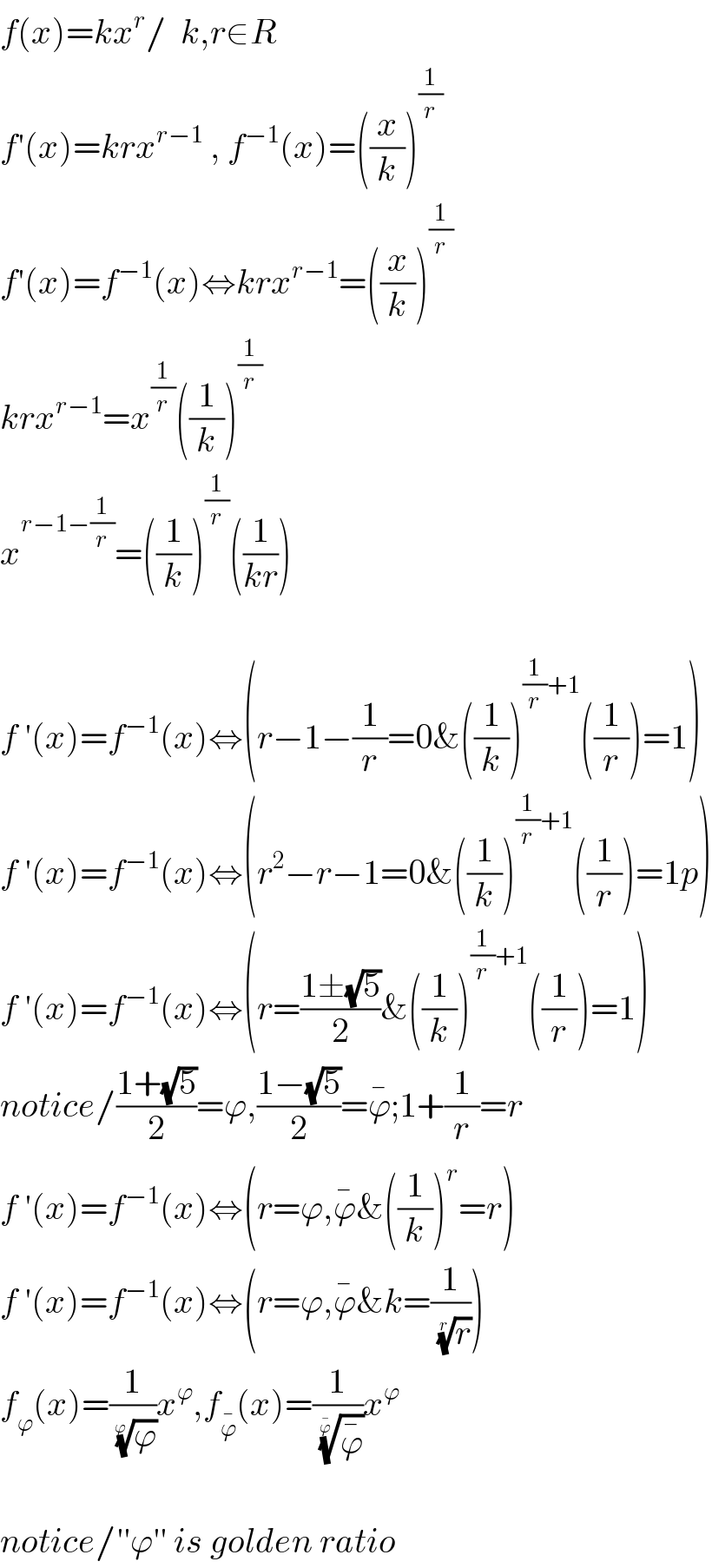
$${f}\left({x}\right)={kx}^{{r}} /\:\:{k},{r}\in{R} \\ $$$${f}'\left({x}\right)={krx}^{{r}−\mathrm{1}} \:,\:{f}^{−\mathrm{1}} \left({x}\right)=\left(\frac{{x}}{{k}}\right)^{\frac{\mathrm{1}}{{r}}} \\ $$$${f}'\left({x}\right)={f}^{−\mathrm{1}} \left({x}\right)\Leftrightarrow{krx}^{{r}−\mathrm{1}} =\left(\frac{{x}}{{k}}\right)^{\frac{\mathrm{1}}{{r}}} \\ $$$${krx}^{{r}−\mathrm{1}} ={x}^{\frac{\mathrm{1}}{{r}}} \left(\frac{\mathrm{1}}{{k}}\right)^{\frac{\mathrm{1}}{{r}}} \\ $$$${x}^{{r}−\mathrm{1}−\frac{\mathrm{1}}{{r}}} =\left(\frac{\mathrm{1}}{{k}}\right)^{\frac{\mathrm{1}}{{r}}} \left(\frac{\mathrm{1}}{{kr}}\right) \\ $$$$ \\ $$$${f}\:'\left({x}\right)={f}^{−\mathrm{1}} \left({x}\right)\Leftrightarrow\left({r}−\mathrm{1}−\frac{\mathrm{1}}{{r}}=\mathrm{0\&}\left(\frac{\mathrm{1}}{{k}}\right)^{\frac{\mathrm{1}}{{r}}+\mathrm{1}} \left(\frac{\mathrm{1}}{{r}}\right)=\mathrm{1}\right) \\ $$$${f}\:'\left({x}\right)={f}^{−\mathrm{1}} \left({x}\right)\Leftrightarrow\left({r}^{\mathrm{2}} −{r}−\mathrm{1}=\mathrm{0\&}\left(\frac{\mathrm{1}}{{k}}\right)^{\frac{\mathrm{1}}{{r}}+\mathrm{1}} \left(\frac{\mathrm{1}}{{r}}\right)=\mathrm{1}{p}\right) \\ $$$${f}\:'\left({x}\right)={f}^{−\mathrm{1}} \left({x}\right)\Leftrightarrow\left({r}=\frac{\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{2}}\&\left(\frac{\mathrm{1}}{{k}}\right)^{\frac{\mathrm{1}}{{r}}+\mathrm{1}} \left(\frac{\mathrm{1}}{{r}}\right)=\mathrm{1}\right) \\ $$$${notice}/\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}=\varphi,\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}=\bar {\varphi};\mathrm{1}+\frac{\mathrm{1}}{{r}}={r} \\ $$$${f}\:'\left({x}\right)={f}^{−\mathrm{1}} \left({x}\right)\Leftrightarrow\left({r}=\varphi,\bar {\varphi}\&\left(\frac{\mathrm{1}}{{k}}\right)^{{r}} ={r}\right) \\ $$$${f}\:'\left({x}\right)={f}^{−\mathrm{1}} \left({x}\right)\Leftrightarrow\left({r}=\varphi,\bar {\varphi}\&{k}=\frac{\mathrm{1}}{\:\sqrt[{{r}}]{{r}}}\right) \\ $$$${f}_{\varphi} \left({x}\right)=\frac{\mathrm{1}}{\:\sqrt[{\varphi}]{\varphi}}{x}^{\varphi} ,{f}_{\bar {\varphi}} \left({x}\right)=\frac{\mathrm{1}}{\:\sqrt[{\bar {\varphi}}]{\bar {\varphi}}}{x}^{\varphi} \\ $$$$ \\ $$$${notice}/''\varphi''\:{is}\:{golden}\:{ratio} \\ $$
Commented by mr W last updated on 15/May/20
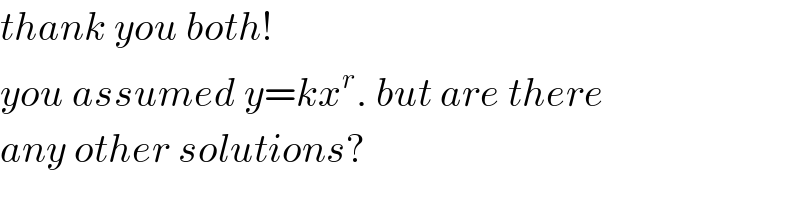
$${thank}\:{you}\:{both}! \\ $$$${you}\:{assumed}\:{y}={kx}^{{r}} .\:{but}\:{are}\:{there} \\ $$$${any}\:{other}\:{solutions}? \\ $$
Commented by M±th+et+s last updated on 15/May/20
$${mybe}\:{there}\:{is},\:{but}\:{i}\:{couldn}'{t}\:{find}\:{just}\:{this} \\ $$
Answered by hovero clinton last updated on 15/May/20