Question Number 112844 by bemath last updated on 10/Sep/20
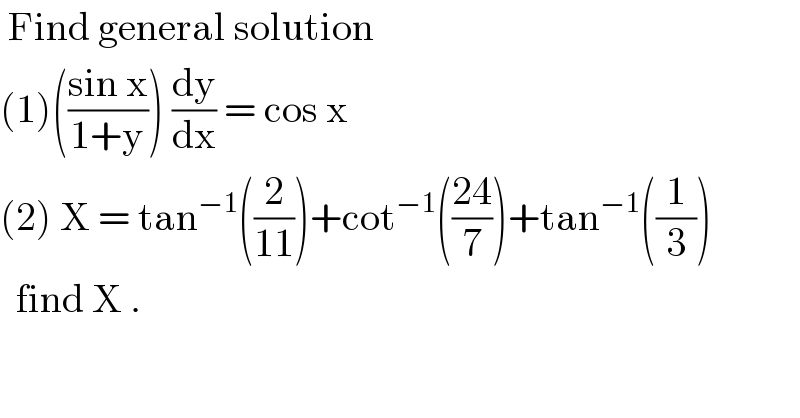
$$\:\mathrm{Find}\:\mathrm{general}\:\mathrm{solution} \\ $$$$\left(\mathrm{1}\right)\left(\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{1}+\mathrm{y}}\right)\:\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\mathrm{cos}\:\mathrm{x} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{X}\:=\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}}{\mathrm{11}}\right)+\mathrm{cot}^{−\mathrm{1}} \left(\frac{\mathrm{24}}{\mathrm{7}}\right)+\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$$\:\:\mathrm{find}\:\mathrm{X}\:. \\ $$
Commented by bemath last updated on 12/Sep/20

Answered by john santu last updated on 10/Sep/20

$$\left(\mathrm{2}\right)\:{first}\:{step}. \\ $$$$\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}}{\mathrm{11}}\right)+\mathrm{cot}^{−\mathrm{1}} \left(\frac{\mathrm{24}}{\mathrm{7}}\right)\:=\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}}{\mathrm{11}}\right)+\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{7}}{\mathrm{24}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:=\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\frac{\mathrm{2}}{\mathrm{11}}+\frac{\mathrm{7}}{\mathrm{24}}}{\mathrm{1}−\frac{\mathrm{2}}{\mathrm{11}}.\frac{\mathrm{7}}{\mathrm{24}}}\right)\:=\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$${second}\:{step}\: \\ $$$${X}\:=\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$${X}=\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{1}}{\mathrm{3}}}\right)\:=\:\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{1}\right) \\ $$$${X}\:=\:\frac{\pi}{\mathrm{4}}. \\ $$$$\:\:\frac{{JS}}{{a}\:{math}\:{farmer}} \\ $$
Answered by bemath last updated on 10/Sep/20

