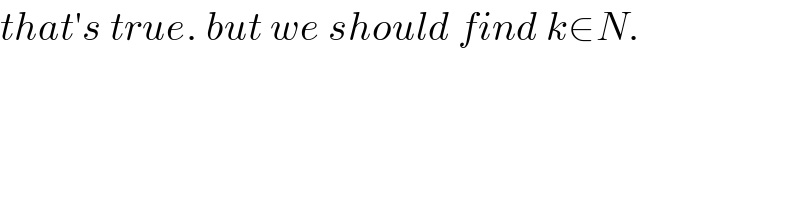Question Number 80580 by mr W last updated on 04/Feb/20

Answered by Rio Michael last updated on 04/Feb/20

Commented by mr W last updated on 04/Feb/20
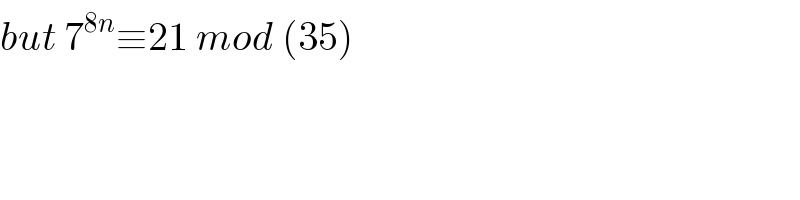
Commented by mr W last updated on 04/Feb/20
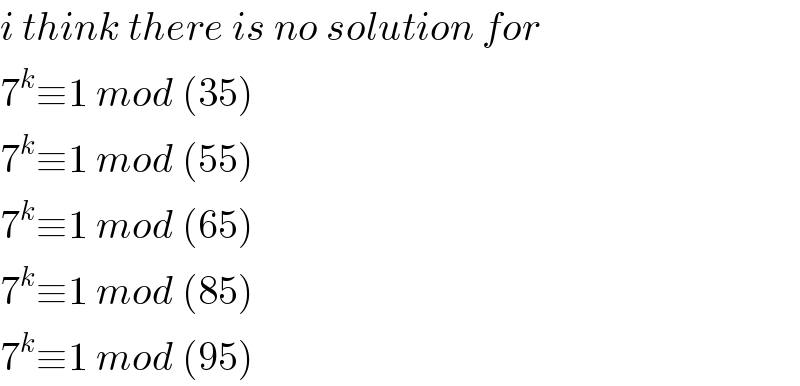
Commented by Rio Michael last updated on 04/Feb/20

Commented by mr W last updated on 04/Feb/20

Commented by Rio Michael last updated on 04/Feb/20

Commented by otchereabdullai@gmail.com last updated on 05/Feb/20
Answered by rkdbdb last updated on 04/Feb/20

Commented by mr W last updated on 05/Feb/20