Question Number 175464 by nadovic last updated on 31/Aug/22

$$\:\mathrm{Find}\:\mathrm{general}\:\mathrm{solutions}\:\mathrm{the}\:\mathrm{following}\: \\ $$$$\mathrm{differential}\:\mathrm{equations} \\ $$$$\left({a}\right)\:\:\:\:\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:+\:\frac{{dy}}{{dx}}\:=\:\mathrm{6}{y} \\ $$$$\left(\mathrm{b}\right)\:\:\:\left(\mathrm{3}{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right){dx}\:+\:\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right){dy}\:=\:\mathrm{0} \\ $$$$ \\ $$
Answered by floor(10²Eta[1]) last updated on 31/Aug/22
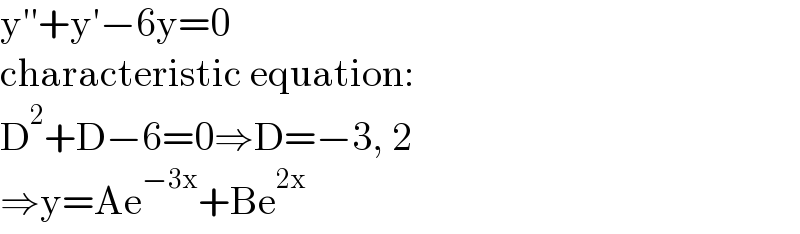
$$\mathrm{y}''+\mathrm{y}'−\mathrm{6y}=\mathrm{0} \\ $$$$\mathrm{characteristic}\:\mathrm{equation}: \\ $$$$\mathrm{D}^{\mathrm{2}} +\mathrm{D}−\mathrm{6}=\mathrm{0}\Rightarrow\mathrm{D}=−\mathrm{3},\:\mathrm{2} \\ $$$$\Rightarrow\mathrm{y}=\mathrm{Ae}^{−\mathrm{3x}} +\mathrm{Be}^{\mathrm{2x}} \\ $$
Answered by floor(10²Eta[1]) last updated on 31/Aug/22

$$\mathrm{y}\left(\mathrm{x}\right)=\mathrm{xv}\left(\mathrm{x}\right) \\ $$$$\mathrm{y}'\left(\mathrm{x}\right)=\mathrm{v}\left(\mathrm{x}\right)+\mathrm{xv}'\left(\mathrm{x}\right)\Rightarrow\frac{\mathrm{dy}}{\mathrm{dx}}=\mathrm{v}+\mathrm{x}\frac{\mathrm{dv}}{\mathrm{dx}} \\ $$$$\mathrm{dy}=\mathrm{vdx}+\mathrm{xdv} \\ $$$$\left(\mathrm{3x}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} \mathrm{v}^{\mathrm{2}} \right)\mathrm{dx}+\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} \mathrm{v}^{\mathrm{2}} \right)\left(\mathrm{vdx}+\mathrm{xdv}\right) \\ $$$$\left(\mathrm{3x}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} \mathrm{v}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} \mathrm{v}+\mathrm{x}^{\mathrm{2}} \mathrm{v}^{\mathrm{3}} \right)\mathrm{dx}+\left(\mathrm{x}^{\mathrm{3}} +\mathrm{x}^{\mathrm{3}} \mathrm{v}^{\mathrm{2}} \right)\mathrm{dv}=\mathrm{0} \\ $$$$\left(\mathrm{3}+\mathrm{v}^{\mathrm{2}} +\mathrm{v}+\mathrm{v}^{\mathrm{3}} \right)\mathrm{dx}+\left(\mathrm{x}+\mathrm{xv}^{\mathrm{2}} \right)\mathrm{dv}=\mathrm{0} \\ $$$$\frac{\mathrm{dv}}{\mathrm{dx}}=−\frac{\mathrm{v}^{\mathrm{3}} +\mathrm{v}^{\mathrm{2}} +\mathrm{v}+\mathrm{3}}{\mathrm{x}\left(\mathrm{v}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$$−\frac{\mathrm{v}^{\mathrm{2}} +\mathrm{1}}{\mathrm{v}^{\mathrm{3}} +\mathrm{v}^{\mathrm{2}} +\mathrm{v}+\mathrm{3}}\mathrm{dv}=\frac{\mathrm{dx}}{\mathrm{x}} \\ $$$$−\int\frac{\mathrm{v}^{\mathrm{2}} +\mathrm{1}}{\mathrm{v}^{\mathrm{3}} +\mathrm{v}^{\mathrm{2}} +\mathrm{v}+\mathrm{3}}\mathrm{dv}=\int\frac{\mathrm{dx}}{\mathrm{x}} \\ $$
