Question Number 25814 by rita1608 last updated on 15/Dec/17
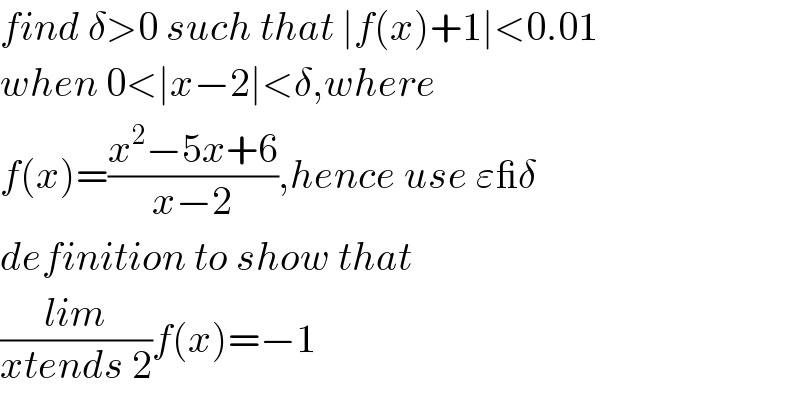
$${find}\:\delta>\mathrm{0}\:{such}\:{that}\:\mid{f}\left({x}\right)+\mathrm{1}\mid<\mathrm{0}.\mathrm{01} \\ $$$${when}\:\mathrm{0}<\mid{x}−\mathrm{2}\mid<\delta,{where} \\ $$$${f}\left({x}\right)=\frac{{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{6}}{{x}−\mathrm{2}},{hence}\:{use}\:\varepsilon\_\delta\:\: \\ $$$${definition}\:{to}\:{show}\:{that}\: \\ $$$$\frac{{lim}}{{xtends}\:\mathrm{2}}{f}\left({x}\right)=−\mathrm{1} \\ $$
Answered by ajfour last updated on 15/Dec/17
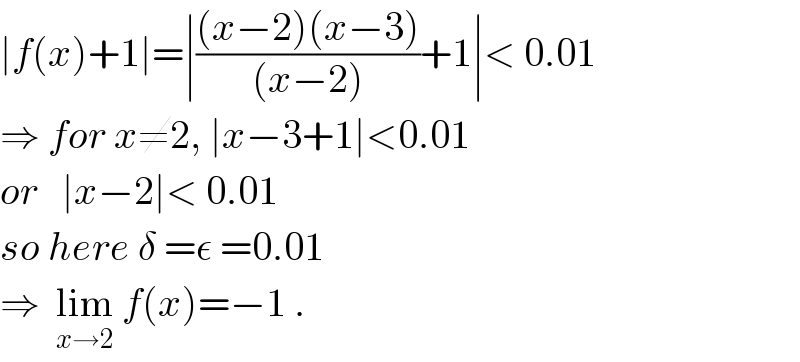
$$\mid{f}\left({x}\right)+\mathrm{1}\mid=\mid\frac{\left({x}−\mathrm{2}\right)\left({x}−\mathrm{3}\right)}{\left({x}−\mathrm{2}\right)}+\mathrm{1}\mid<\:\mathrm{0}.\mathrm{01} \\ $$$$\Rightarrow\:{for}\:{x}\neq\mathrm{2},\:\mid{x}−\mathrm{3}+\mathrm{1}\mid<\mathrm{0}.\mathrm{01} \\ $$$${or}\:\:\:\mid{x}−\mathrm{2}\mid<\:\mathrm{0}.\mathrm{01} \\ $$$${so}\:{here}\:\delta\:=\epsilon\:=\mathrm{0}.\mathrm{01} \\ $$$$\Rightarrow\:\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:{f}\left({x}\right)=−\mathrm{1}\:. \\ $$
Commented by kaivan.ahmadi last updated on 15/Dec/17

$$\delta\leqslant\epsilon\:\mathrm{and}\:\mathrm{Max}\left(\delta\right)=\mathrm{0}.\mathrm{01} \\ $$
