Question Number 119752 by Bird last updated on 26/Oct/20
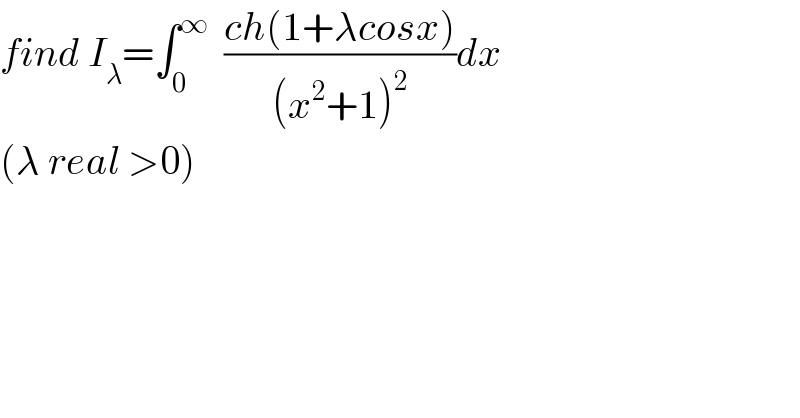
$${find}\:{I}_{\lambda} =\int_{\mathrm{0}} ^{\infty} \:\:\frac{{ch}\left(\mathrm{1}+\lambda{cosx}\right)}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$$$\left(\lambda\:{real}\:>\mathrm{0}\right) \\ $$
Answered by mathmax by abdo last updated on 27/Oct/20

$$\mathrm{I}_{\lambda} =\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{ch}\left(\mathrm{1}+\lambda\mathrm{cosx}\right)}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}\:\:\Rightarrow\mathrm{I}_{\lambda} =\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{e}^{\mathrm{1}+\lambda\mathrm{cosx}} +\mathrm{e}^{−\left(\mathrm{1}+\lambda\mathrm{cosx}\right)} }{\mathrm{2}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$=\frac{\mathrm{e}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{\lambda\mathrm{cosx}} }{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}\:+\frac{\mathrm{1}}{\mathrm{2e}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\lambda\mathrm{cosx}} }{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}\:=\frac{\mathrm{e}}{\mathrm{2}}\mathrm{A}\:+\frac{\mathrm{1}}{\mathrm{2e}}\mathrm{B} \\ $$$$\mathrm{A}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{\lambda\mathrm{cosx}} }{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}\Rightarrow\mathrm{A}\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{−\infty} ^{+\infty} \:\frac{\mathrm{e}^{\lambda\mathrm{cosx}} }{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$\mathrm{let}\:\varphi\left(\mathrm{z}\right)=\frac{\mathrm{e}^{\lambda\mathrm{cosz}} }{\left(\mathrm{z}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow\varphi\left(\mathrm{z}\right)=\frac{\mathrm{e}^{\lambda\mathrm{cosz}} }{\left(\mathrm{z}−\mathrm{i}\right)^{\mathrm{2}} \left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{2}} } \\ $$$$\int_{−\infty} ^{+\infty} \varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\:\mathrm{Res}\left(\varphi,\mathrm{i}\right) \\ $$$$\mathrm{Res}\left(\varphi,\mathrm{i}\right)\:=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{1}\right)!}\left\{\left(\mathrm{z}−\mathrm{i}\right)^{\mathrm{2}} \varphi\left(\mathrm{z}\right)\right\}^{\left(\mathrm{1}\right)} \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\:\:\left\{\:\frac{\mathrm{e}^{\lambda\mathrm{cosz}} }{\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{2}} }\right\}^{\left(\mathrm{1}\right)} =\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\:\frac{−\lambda\mathrm{sinze}^{\lambda\mathrm{cosz}} \left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{2}} −\mathrm{2}\left(\mathrm{z}+\mathrm{i}\right)\mathrm{e}^{\lambda\mathrm{cosz}} }{\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{4}} } \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\frac{−\lambda\mathrm{sinze}^{\lambda\mathrm{cosz}} \left(\mathrm{z}+\mathrm{i}\right)−\mathrm{2}\:\mathrm{e}^{\lambda\mathrm{cosz}} }{\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{3}} } \\ $$$$=\frac{−\lambda\mathrm{sinie}^{\lambda\mathrm{cos}\left(\mathrm{i}\right)} \left(\mathrm{2i}\right)−\mathrm{2e}^{\lambda\mathrm{cos}\left(\mathrm{i}\right)} }{−\mathrm{8i}}\:=\frac{\lambda\mathrm{sin}\left(\mathrm{i}\right)\mathrm{e}^{\lambda\mathrm{cos}\left(\mathrm{i}\right)} \:+\mathrm{e}^{\lambda\mathrm{cos}\left(\mathrm{i}\right)} }{\mathrm{4i}}\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi×\frac{\left(\mathrm{1}+\lambda\mathrm{sin}\left(\mathrm{i}\right)\right)\mathrm{e}^{\lambda\mathrm{cos}\left(\mathrm{i}\right)} }{\mathrm{4i}} \\ $$$$=\frac{\pi}{\mathrm{2}}\left(\mathrm{1}+\lambda\mathrm{sh}\left(−\mathrm{1}\right)\right)\mathrm{e}^{\lambda\mathrm{ch}\left(−\mathrm{1}\right)} \:=\frac{\pi}{\mathrm{2}}\left(\mathrm{1}−\lambda\mathrm{sh}\left(\mathrm{1}\right)\right)\mathrm{e}^{\lambda\mathrm{ch}\left(\mathrm{1}\right)} \:\Rightarrow \\ $$$$\mathrm{A}\:=\frac{\pi}{\mathrm{4}}\left(\mathrm{1}−\lambda\mathrm{sh}\left(\mathrm{1}\right)\right)\mathrm{e}^{\lambda\mathrm{ch}\left(\mathrm{1}\right)} \:\:\mathrm{also} \\ $$$$\mathrm{B}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\lambda\mathrm{cosx}} }{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{\pi}{\mathrm{4}}\left(\mathrm{1}+\lambda\mathrm{sh}\left(\mathrm{1}\right)\right)\mathrm{e}^{−\lambda\mathrm{ch}\left(\mathrm{1}\right)} \:\:\:\:\left(\mathrm{change}\:\lambda\:\mathrm{by}\:−\lambda\right)\:\Rightarrow \\ $$$$\mathrm{I}\:=\frac{\pi\mathrm{e}}{\mathrm{8}}\left(\mathrm{1}−\lambda\mathrm{sh}\left(\mathrm{1}\right)\right)\mathrm{e}^{\lambda\mathrm{ch}\left(\mathrm{1}\right)} \:+\frac{\pi\mathrm{e}^{−\mathrm{1}} }{\mathrm{8}}\left(\mathrm{1}+\lambda\mathrm{sh}\left(\mathrm{1}\right)\right)\mathrm{e}^{−\lambda\mathrm{ch}\left(\mathrm{1}\right)} \\ $$$$ \\ $$
