Question Number 38116 by maxmathsup by imad last updated on 21/Jun/18
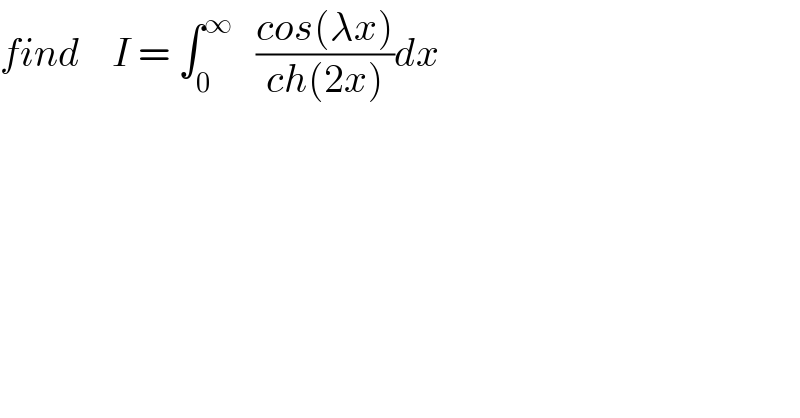
$${find}\:\:\:\:{I}\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{cos}\left(\lambda{x}\right)}{{ch}\left(\mathrm{2}{x}\right)}{dx}\: \\ $$
Commented by prof Abdo imad last updated on 29/Jun/18
![I = 2 ∫_0 ^∞ ((cos(λx))/(e^(2x) +e^(−2x) ))dx =2 ∫_0 ^∞ ((e^(−2x) cos(λx))/(1+e^(−4x) ))dx =2 ∫_0 ^∞ e^(−2x) cos(λx)(Σ_(n=0) ^∞ (−1)^n e^(−4nx) )dx =2 Σ_(n=0) ^∞ (−1)^n ∫_0 ^∞ e^(−(2+4n)x) cos(λx)dx =2 Σ_(n=0) ^∞ (−1)^n A_n A_n =Re( ∫_0 ^∞ e^(−(2+4n)x +iλx) dx) but ∫_0 ^∞ e^({−(2+4n)+iλ)x) dx=[(1/(−(2+4n)+iλ))e^({−(2+4n)+iλ}x) ]_0 ^(+∞) = (1/(2+4n−iλ)) =((2+4n +iλ)/((2+4n)^2 +λ^2 )) ⇒ A_n = ((2+4n)/((2+4n)^2 +λ^2 )) ⇒ I = 2Σ_(n=0) ^∞ (−1)^n ((2+4n)/((2+4n)^(2 ) +λ^2 )) this serie will be calculalated by sir fourier ..will be continued...](https://www.tinkutara.com/question/Q38757.png)
$${I}\:=\:\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{cos}\left(\lambda{x}\right)}{{e}^{\mathrm{2}{x}} \:+{e}^{−\mathrm{2}{x}} }{dx} \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{e}^{−\mathrm{2}{x}} {cos}\left(\lambda{x}\right)}{\mathrm{1}+{e}^{−\mathrm{4}{x}} }{dx} \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−\mathrm{2}{x}} {cos}\left(\lambda{x}\right)\left(\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} \:{e}^{−\mathrm{4}{nx}} \right){dx} \\ $$$$=\mathrm{2}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} \:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−\left(\mathrm{2}+\mathrm{4}{n}\right){x}} {cos}\left(\lambda{x}\right){dx} \\ $$$$=\mathrm{2}\:\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} \:{A}_{{n}} \\ $$$${A}_{{n}} ={Re}\left(\:\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−\left(\mathrm{2}+\mathrm{4}{n}\right){x}\:+{i}\lambda{x}} {dx}\right)\:{but} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:{e}^{\left\{−\left(\mathrm{2}+\mathrm{4}{n}\right)+{i}\lambda\right){x}} {dx}=\left[\frac{\mathrm{1}}{−\left(\mathrm{2}+\mathrm{4}{n}\right)+{i}\lambda}{e}^{\left\{−\left(\mathrm{2}+\mathrm{4}{n}\right)+{i}\lambda\right\}{x}} \right]_{\mathrm{0}} ^{+\infty} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}+\mathrm{4}{n}−{i}\lambda}\:=\frac{\mathrm{2}+\mathrm{4}{n}\:+{i}\lambda}{\left(\mathrm{2}+\mathrm{4}{n}\right)^{\mathrm{2}} \:+\lambda^{\mathrm{2}} }\:\Rightarrow \\ $$$${A}_{{n}} =\:\frac{\mathrm{2}+\mathrm{4}{n}}{\left(\mathrm{2}+\mathrm{4}{n}\right)^{\mathrm{2}} \:+\lambda^{\mathrm{2}} }\:\Rightarrow \\ $$$${I}\:=\:\mathrm{2}\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} \:\:\:\:\frac{\mathrm{2}+\mathrm{4}{n}}{\left(\mathrm{2}+\mathrm{4}{n}\right)^{\mathrm{2}\:} \:+\lambda^{\mathrm{2}} } \\ $$$${this}\:{serie}\:{will}\:{be}\:{calculalated}\:{by}\:{sir}\:{fourier} \\ $$$$..{will}\:{be}\:{continued}… \\ $$$$ \\ $$
