Question Number 27187 by abdo imad last updated on 02/Jan/18
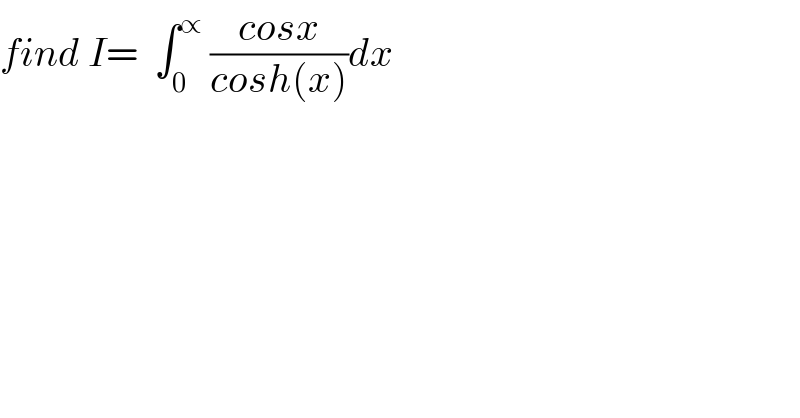
$${find}\:{I}=\:\:\int_{\mathrm{0}} ^{\propto} \:\frac{{cosx}}{{cosh}\left({x}\right)}{dx} \\ $$
Commented by abdo imad last updated on 08/Jan/18
![I= ∫_0 ^∞ ((cosx)/((e^x +e^(−x) )/2))dx= 2 ∫_0 ^∞ (e^(−x) /(1+e^(−2x) ))cosx dx =2∫_0 ^∞ e^(−x) (Σ_(n=0) ^∝ e^(−2nx) )cosxdx =2 Σ_(n=0) ^∝ ∫_0 ^∞ e^(−(2n+1)x) cosxdx but let calculate ∫_0 ^∞ e^(−ax) cosx dx with a>0 ∫_0 ^∞ e^(−ax) cosx dx= Re (∫_0 ^∞ e^((i−a)x) dx) and ∫_0 ^∞ e^((i−a)x) dx = [ (1/(i−a)) e^((i−a)x) ]_(x=0) ^(x−>∝) = −(1/(i−a))= (1/(a−i)) =((a+i)/(a^2 +1)) ⇒∫_0 ^∞ e^(−ax) cosxdx= (a/(1+a^2 )) so ∫_0 ^∞ e^(−(2n+1)x) cosx dx=((2n+1)/(1+(2n+1)^2 )) I=2Σ_(n=0) ^∝ ((2n+1)/(1+(2n+1)^2 )) and this sum is calculated by fourier series...be continued....](https://www.tinkutara.com/question/Q27549.png)
$${I}=\:\int_{\mathrm{0}} ^{\infty} \:\frac{{cosx}}{\frac{{e}^{{x}} \:+{e}^{−{x}} }{\mathrm{2}}}{dx}=\:\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{x}} }{\mathrm{1}+{e}^{−\mathrm{2}{x}} }{cosx}\:{dx} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:{e}^{−{x}} \left(\sum_{{n}=\mathrm{0}} ^{\propto} \:{e}^{−\mathrm{2}{nx}} \right){cosxdx} \\ $$$$=\mathrm{2}\:\sum_{{n}=\mathrm{0}} ^{\propto} \:\int_{\mathrm{0}} ^{\infty} \:{e}^{−\left(\mathrm{2}{n}+\mathrm{1}\right){x}} {cosxdx}\:{but} \\ $$$${let}\:{calculate}\:\int_{\mathrm{0}} ^{\infty} \:{e}^{−{ax}} {cosx}\:{dx}\:\:\:{with}\:{a}>\mathrm{0} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:{e}^{−{ax}} {cosx}\:{dx}=\:{Re}\:\left(\int_{\mathrm{0}} ^{\infty} \:{e}^{\left({i}−{a}\right){x}} {dx}\right)\:{and} \\ $$$$\:\int_{\mathrm{0}} ^{\infty} \:{e}^{\left({i}−{a}\right){x}} {dx}\:=\:\left[\:\frac{\mathrm{1}}{{i}−{a}}\:{e}^{\left({i}−{a}\right){x}} \right]_{{x}=\mathrm{0}} ^{{x}−>\propto} =\:−\frac{\mathrm{1}}{{i}−{a}}=\:\frac{\mathrm{1}}{{a}−{i}} \\ $$$$=\frac{{a}+{i}}{{a}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow\int_{\mathrm{0}} ^{\infty} \:{e}^{−{ax}} {cosxdx}=\:\frac{{a}}{\mathrm{1}+{a}^{\mathrm{2}} }\:{so} \\ $$$$\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−\left(\mathrm{2}{n}+\mathrm{1}\right){x}} {cosx}\:{dx}=\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{1}+\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${I}=\mathrm{2}\sum_{{n}=\mathrm{0}} ^{\propto} \:\:\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{1}+\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:{and}\:{this}\:{sum}\:{is}\:{calculated}\:{by}\:{fourier} \\ $$$${series}…{be}\:{continued}…. \\ $$$$ \\ $$
