Question Number 146363 by mathmax by abdo last updated on 13/Jul/21
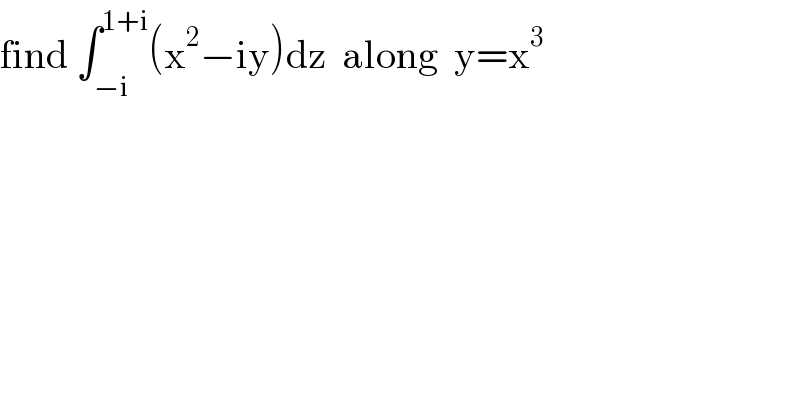
$$\mathrm{find}\:\int_{−\mathrm{i}} ^{\mathrm{1}+\mathrm{i}} \left(\mathrm{x}^{\mathrm{2}} −\mathrm{iy}\right)\mathrm{dz}\:\:\mathrm{along}\:\:\mathrm{y}=\mathrm{x}^{\mathrm{3}} \\ $$
Answered by mathmax by abdo last updated on 13/Jul/21
![Υ=∫_(−i) ^(1+i) (x^2 −iy)dz =∫_((0,−1)) ^((1,1)) (x^2 −iy)(dx+idy) (z=x+iy) y=x^3 ⇒dy=3x^2 dx ⇒Υ=∫_0 ^1 (x^2 −ix^3 )(dx+i3x^2 dx) =∫_0 ^1 x^2 (1−ix)(1+3ix^2 )dx =∫_0 ^1 x^2 (1+3ix^2 −ix+3x^2 )dx =∫_0 ^1 (x^2 +3ix^4 −ix^3 +3x^4 )dx =[(x^3 /3)+((3i)/5)x^5 −(i/4)x^4 +(3/5)x^5 ]_0 ^1 =(1/3)+(3/5)i−(1/4)i+(3/5)=((14)/(15)) +(7/(20))i](https://www.tinkutara.com/question/Q146456.png)
$$\Upsilon=\int_{−\mathrm{i}} ^{\mathrm{1}+\mathrm{i}} \:\left(\mathrm{x}^{\mathrm{2}} −\mathrm{iy}\right)\mathrm{dz}\:\:=\int_{\left(\mathrm{0},−\mathrm{1}\right)} ^{\left(\mathrm{1},\mathrm{1}\right)} \left(\mathrm{x}^{\mathrm{2}} −\mathrm{iy}\right)\left(\mathrm{dx}+\mathrm{idy}\right)\:\left(\mathrm{z}=\mathrm{x}+\mathrm{iy}\right) \\ $$$$\mathrm{y}=\mathrm{x}^{\mathrm{3}} \:\Rightarrow\mathrm{dy}=\mathrm{3x}^{\mathrm{2}} \:\mathrm{dx}\:\Rightarrow\Upsilon=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{x}^{\mathrm{2}} −\mathrm{ix}^{\mathrm{3}} \right)\left(\mathrm{dx}+\mathrm{i3x}^{\mathrm{2}} \mathrm{dx}\right) \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{x}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{ix}\right)\left(\mathrm{1}+\mathrm{3ix}^{\mathrm{2}} \right)\mathrm{dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{x}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{3ix}^{\mathrm{2}} −\mathrm{ix}+\mathrm{3x}^{\mathrm{2}} \right)\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{3ix}^{\mathrm{4}} −\mathrm{ix}^{\mathrm{3}} +\mathrm{3x}^{\mathrm{4}} \right)\mathrm{dx}\:=\left[\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{\mathrm{3i}}{\mathrm{5}}\mathrm{x}^{\mathrm{5}} \:−\frac{\mathrm{i}}{\mathrm{4}}\mathrm{x}^{\mathrm{4}} \:+\frac{\mathrm{3}}{\mathrm{5}}\mathrm{x}^{\mathrm{5}} \right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{3}}{\mathrm{5}}\mathrm{i}−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{i}+\frac{\mathrm{3}}{\mathrm{5}}=\frac{\mathrm{14}}{\mathrm{15}}\:+\frac{\mathrm{7}}{\mathrm{20}}\mathrm{i} \\ $$
