Question Number 79094 by mathmax by abdo last updated on 22/Jan/20
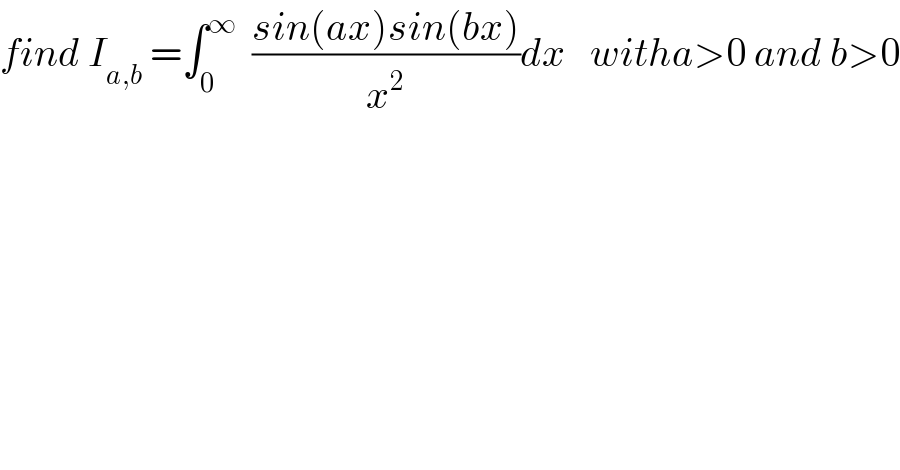
$${find}\:{I}_{{a},{b}} \:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{sin}\left({ax}\right){sin}\left({bx}\right)}{{x}^{\mathrm{2}} }{dx}\:\:\:{witha}>\mathrm{0}\:{and}\:{b}>\mathrm{0} \\ $$
Answered by mind is power last updated on 23/Jan/20
![2sin(ax)sin(bx)=cos((a−b)x)−cos((a+b)x) f(z)=∫_0 ^(+∞) ((cos(zx)−1)/x^2 ) dx z∈R well defind in zero cos(zx)−1=−((z^2 x^2 )/2)+o(x^3 ) for z>1 ((∣cos(zx)−1∣)/x^2 )≤(2/x^2 ),integrabl in [1,+∞[ ∀(z,x)∈IR×R^∗ (z,x)→((cos(zx)−1)/x^2 ) ∈C_∞ C_1 is what we need (∂/∂z)(((cos(zx)−1)/x^2 ))=−((sin(zx))/x)∈C_1 ]0,+∞[ ∫_0 ^(+∞) −((sin(zx))/x)dx <∞ ⇒f(z)∈C_1 f′(z)=∫_0 ^(+∞) (∂/∂z)(((cos(zx)−1)/x^2 ))=−∫_0 ^(+∞) ((sin(zx))/x)dx,u=zx if z>0 =−∫_0 ^(+∞) ((sin(u))/u)du=−(π/2),z<0 =(π/2) ⇒f′(z)=−sign(z)(π/2) f(z)=−((zsign(z)π)/2)+c f(0)=0⇒c=0 f(z)=((−zsign(z)π)/2) I_(a,b) =∫_0 ^(+∞) ((sin(ax)sin(bx))/x^2 )dx =∫_0 ^(+∞) ((cos((a−b)x)−cos((a+b)x))/(2x^2 ))dx =∫_0 ^(+∞) ((cos((a−b)x)−1−(cos((a+b)x)−1))/(2x^2 ))dx =(1/2)∫_0 ^(+∞) ((cos((a−b)x)−1)/x^2 )−(1/2)∫_0 ^(+∞) ((cos((a+b)x)−1)/x^2 ) =(1/2)f((a−b))−(1/2)f(a+b))=−(((a−b)sivn(a−b)π)/4)+(((a+b)sign(a+b)π)/4) =(π/4)((a+b)sign(a+b)−(a−b)sign(a−b))](https://www.tinkutara.com/question/Q79197.png)
$$\mathrm{2}{sin}\left({ax}\right){sin}\left({bx}\right)={cos}\left(\left({a}−{b}\right){x}\right)−{cos}\left(\left({a}+{b}\right){x}\right) \\ $$$${f}\left({z}\right)=\int_{\mathrm{0}} ^{+\infty} \frac{{cos}\left({zx}\right)−\mathrm{1}}{{x}^{\mathrm{2}} }\:{dx} \\ $$$${z}\in\mathbb{R}\:\:{well}\:{defind} \\ $$$${in}\:{zero}\:\:{cos}\left({zx}\right)−\mathrm{1}=−\frac{{z}^{\mathrm{2}} {x}^{\mathrm{2}} }{\mathrm{2}}+{o}\left({x}^{\mathrm{3}} \right) \\ $$$${for}\:{z}>\mathrm{1}\:\:\frac{\mid{cos}\left({zx}\right)−\mathrm{1}\mid}{{x}^{\mathrm{2}} }\leqslant\frac{\mathrm{2}}{{x}^{\mathrm{2}} },{integrabl}\:{in}\:\left[\mathrm{1},+\infty\left[\right.\right. \\ $$$$\forall\left({z},{x}\right)\in{IR}×\mathbb{R}^{\ast} \left({z},{x}\right)\rightarrow\frac{{cos}\left({zx}\right)−\mathrm{1}}{{x}^{\mathrm{2}} }\:\:\:\in{C}_{\infty} \:\:{C}_{\mathrm{1}} \:{is}\:{what}\:{we}\:{need} \\ $$$$\left.\frac{\partial}{\partial{z}}\left(\frac{{cos}\left({zx}\right)−\mathrm{1}}{{x}^{\mathrm{2}} }\right)=−\frac{{sin}\left({zx}\right)}{{x}}\in{C}_{\mathrm{1}} \right]\mathrm{0},+\infty\left[\right. \\ $$$$\int_{\mathrm{0}} ^{+\infty} −\frac{{sin}\left({zx}\right)}{{x}}{dx}\:<\infty\:\:\Rightarrow{f}\left({z}\right)\in{C}_{\mathrm{1}} \\ $$$${f}'\left({z}\right)=\int_{\mathrm{0}} ^{+\infty} \frac{\partial}{\partial{z}}\left(\frac{{cos}\left({zx}\right)−\mathrm{1}}{{x}^{\mathrm{2}} }\right)=−\int_{\mathrm{0}} ^{+\infty} \frac{{sin}\left({zx}\right)}{{x}}{dx},{u}={zx} \\ $$$${if}\:{z}>\mathrm{0} \\ $$$$=−\int_{\mathrm{0}} ^{+\infty} \frac{{sin}\left({u}\right)}{{u}}{du}=−\frac{\pi}{\mathrm{2}},{z}<\mathrm{0}\:\:=\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow{f}'\left({z}\right)=−{sign}\left({z}\right)\frac{\pi}{\mathrm{2}} \\ $$$${f}\left({z}\right)=−\frac{{zsign}\left({z}\right)\pi}{\mathrm{2}}+{c} \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{0}\Rightarrow{c}=\mathrm{0} \\ $$$${f}\left({z}\right)=\frac{−{zsign}\left({z}\right)\pi}{\mathrm{2}} \\ $$$${I}_{{a},{b}} =\int_{\mathrm{0}} ^{+\infty} \frac{{sin}\left({ax}\right){sin}\left({bx}\right)}{{x}^{\mathrm{2}} }{dx} \\ $$$$=\int_{\mathrm{0}} ^{+\infty} \frac{{cos}\left(\left({a}−{b}\right){x}\right)−{cos}\left(\left({a}+{b}\right){x}\right)}{\mathrm{2}{x}^{\mathrm{2}} }{dx} \\ $$$$=\int_{\mathrm{0}} ^{+\infty} \frac{{cos}\left(\left({a}−{b}\right){x}\right)−\mathrm{1}−\left({cos}\left(\left({a}+{b}\right){x}\right)−\mathrm{1}\right)}{\mathrm{2}{x}^{\mathrm{2}} }{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{+\infty} \frac{{cos}\left(\left({a}−{b}\right){x}\right)−\mathrm{1}}{{x}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{+\infty} \frac{{cos}\left(\left({a}+{b}\right){x}\right)−\mathrm{1}}{{x}^{\mathrm{2}} } \\ $$$$\left.=\frac{\mathrm{1}}{\mathrm{2}}{f}\left(\left({a}−{b}\right)\right)−\frac{\mathrm{1}}{\mathrm{2}}{f}\left({a}+{b}\right)\right)=−\frac{\left({a}−{b}\right){sivn}\left({a}−{b}\right)\pi}{\mathrm{4}}+\frac{\left({a}+{b}\right){sign}\left({a}+{b}\right)\pi}{\mathrm{4}} \\ $$$$=\frac{\pi}{\mathrm{4}}\left(\left({a}+{b}\right){sign}\left({a}+{b}\right)−\left({a}−{b}\right){sign}\left({a}−{b}\right)\right) \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by msup trace by abdo last updated on 23/Jan/20

$${thank}\:{you}\:{sir}. \\ $$
