Question Number 27999 by abdo imad last updated on 18/Jan/18
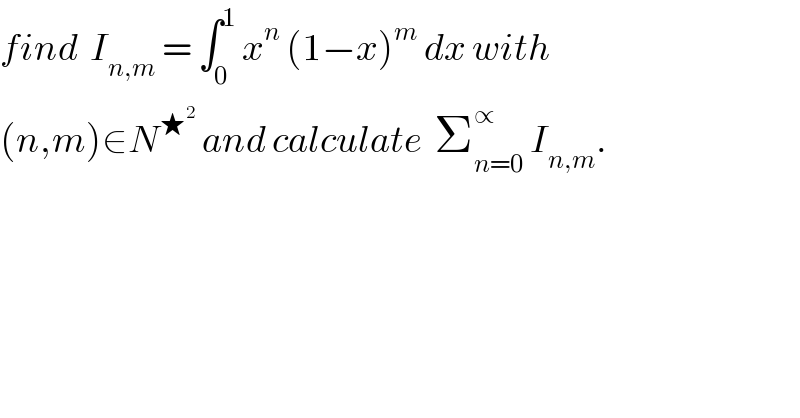
$${find}\:\:{I}_{{n},{m}} \:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{{n}} \:\left(\mathrm{1}−{x}\right)^{{m}} \:{dx}\:{with} \\ $$$$\left({n},{m}\right)\in{N}^{\bigstar^{\mathrm{2}} } \:{and}\:{calculate}\:\:\sum_{{n}=\mathrm{0}} ^{\propto} \:{I}_{{n},{m}} . \\ $$
Commented by abdo imad last updated on 22/Jan/18
![due to uniform convergence we have Σ_(n=0) ^(+∞) I_(n,m) = ∫_0 ^1 (1−x)^m (Σ_(n=0) ^∝ x^n ) = ∫_0 ^1 (((1−x)^m )/(1−x))dx = ∫_0 ^1 (1−x)^(m−1) dx = [((−1)/m)(1−x)^m ]_0 ^1 = (1/m) for m≥1 .let calculate I_(n,m) by parts we have I_(n,m) = [−(1/(m+1)) x^n (1−x)^(m+1) ]_0 ^1 +(1/(m+1))∫_0 ^1 nx^(n−1) (1−x)^(m+1) dx =(n/(m+1)) ∫_0 ^1 x^(n−1) (1−x)^(m+1) dx I_(n,m) =(n/(m+1)) I_(n−1,m+1) = (n/(m+1)) ((n−1)/(m+2)) I_(n−2,m+2) =((n(n−1)....(n−p+1))/((m+1)(m+2)...(m+p))) I_(n−p,m+p) = ((n!)/((m+1)(m+2) ....(m+n))) I_(0,m+n) but I_(0,m+n) =∫_0 ^1 (1−x)^(m+n) dx =[((−1)/(m+n+1))(1−x)^(m+n+1) ]_0 ^1 = (1/(m+n+1)) so I_(n,m) = ((n!)/((m+1)(m+2)...(m+n+1))) I_(n,m) = (((n!)(m!))/((m+n+1)!)) .](https://www.tinkutara.com/question/Q28205.png)
$${due}\:{to}\:{uniform}\:{convergence}\:{we}\:{have} \\ $$$$\sum_{{n}=\mathrm{0}} ^{+\infty} \:{I}_{{n},{m}} \:\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{x}\right)^{{m}} \left(\sum_{{n}=\mathrm{0}} ^{\propto} \:{x}^{{n}} \:\:\right) \\ $$$$=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{\left(\mathrm{1}−{x}\right)^{{m}} }{\mathrm{1}−{x}}{dx}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\left(\mathrm{1}−{x}\right)^{{m}−\mathrm{1}} {dx} \\ $$$$=\:\left[\frac{−\mathrm{1}}{{m}}\left(\mathrm{1}−{x}\right)^{{m}} \right]_{\mathrm{0}} ^{\mathrm{1}} =\:\frac{\mathrm{1}}{{m}}\:\:{for}\:\:{m}\geqslant\mathrm{1}\:\:.{let}\:{calculate}\:{I}_{{n},{m}} \\ $$$${by}\:{parts}\:{we}\:{have}\: \\ $$$${I}_{{n},{m}} =\:\left[−\frac{\mathrm{1}}{{m}+\mathrm{1}}\:{x}^{{n}} \left(\mathrm{1}−{x}\right)^{{m}+\mathrm{1}} \right]_{\mathrm{0}} ^{\mathrm{1}} \:+\frac{\mathrm{1}}{{m}+\mathrm{1}}\int_{\mathrm{0}} ^{\mathrm{1}} {nx}^{{n}−\mathrm{1}} \:\left(\mathrm{1}−{x}\right)^{{m}+\mathrm{1}} {dx} \\ $$$$=\frac{{n}}{{m}+\mathrm{1}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{x}^{{n}−\mathrm{1}} \left(\mathrm{1}−{x}\right)^{{m}+\mathrm{1}} {dx} \\ $$$${I}_{{n},{m}} \:=\frac{{n}}{{m}+\mathrm{1}}\:{I}_{{n}−\mathrm{1},{m}+\mathrm{1}} =\:\frac{{n}}{{m}+\mathrm{1}}\:\frac{{n}−\mathrm{1}}{{m}+\mathrm{2}}\:{I}_{{n}−\mathrm{2},{m}+\mathrm{2}} \\ $$$$=\frac{{n}\left({n}−\mathrm{1}\right)….\left({n}−{p}+\mathrm{1}\right)}{\left({m}+\mathrm{1}\right)\left({m}+\mathrm{2}\right)…\left({m}+{p}\right)}\:{I}_{{n}−{p},{m}+{p}} \\ $$$$=\:\frac{{n}!}{\left({m}+\mathrm{1}\right)\left({m}+\mathrm{2}\right)\:….\left({m}+{n}\right)}\:{I}_{\mathrm{0},{m}+{n}} \:\:{but} \\ $$$${I}_{\mathrm{0},{m}+{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{x}\right)^{{m}+{n}} {dx}\:=\left[\frac{−\mathrm{1}}{{m}+{n}+\mathrm{1}}\left(\mathrm{1}−{x}\right)^{{m}+{n}+\mathrm{1}} \right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\:\frac{\mathrm{1}}{{m}+{n}+\mathrm{1}}\:\:{so} \\ $$$${I}_{{n},{m}} =\:\:\:\:\frac{{n}!}{\left({m}+\mathrm{1}\right)\left({m}+\mathrm{2}\right)…\left({m}+{n}+\mathrm{1}\right)} \\ $$$${I}_{{n},{m}} =\:\:\frac{\left({n}!\right)\left({m}!\right)}{\left({m}+{n}+\mathrm{1}\right)!}\:\:. \\ $$
