Find-image-of-plane-x-y-z-3-0-in-plane-2x-y-z-4-0-

Question Number 45417 by rahul 19 last updated on 12/Oct/18

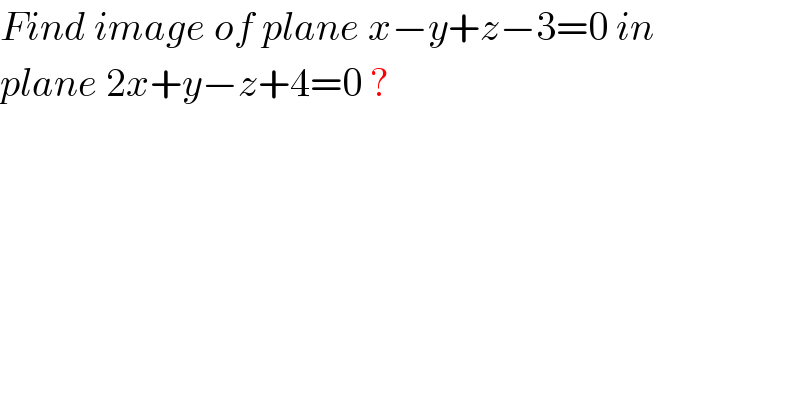
F i n d i m a g e o f p l a n e x - y + z - 3 = 0 i n

p l a n e 2 x + y - z + 4 = 0 ?

Answered by MrW3 last updated on 13/Oct/18

s i n c e b o t h p l a n e s a r e p e r p e n d i c u l a r

t o e a c h o t h e r, t h e i m a g e i s i t s e l f, i . e .

x - y + z - 3 = 0

b u t I^{'} l l s h o w y o u a g e n e r a l w a y t o f i n d

t h e i m a g e i n a p l a n e .

t h e i m a g e o f p o i n t (X, Y, Z) i n p l a n e

a x + b y + c z + d = 0

i s p o i n t (U, V, W) w i t h

U = X - \frac{2 a (a X + b Y + c Z + d)}{a^{2} + b^{2} + c^{2}}

V = Y - \frac{2 b (a X + b Y + c Z + d)}{a^{2} + b^{2} + c^{2}}

W = Z - \frac{2 c (a X + b Y + c Z + d)}{a^{2} + b^{2} + c^{2}}

n o w w e t a k e a p o i n t P (u, v, w) o n t h e p l a n e

x - y + z - 3 = 0

I t s i m a g e i n t h e p l a n e

2 x + y - z + 4 = 0

i s P^{'} (p, q, r) .

w e c a n a l s o s a y P (u, v, w) i s t h e i m a g e

o f P^{'} (p, q, r) . u s i n g f o r m u l a a b o v e w e g e t

u = p - \frac{2 \times 2 (2 p + q - r + 4)}{2^{2} + 1^{2} + {(- 1)}^{2}}

\Rightarrow u = p - \frac{2 (2 p + q - r + 4)}{3}

s i m i l a r l y

\Rightarrow v = q - \frac{1 (2 p + q - r + 4)}{3}

\Rightarrow w = r - \frac{(- 1) (2 p + q - r + 4)}{3}

s i n c e u - v + w - 3 = 0

p - \frac{2 (2 p + q - r + 4)}{3} - q + \frac{(2 p + q - r + 4)}{3} + r + \frac{(2 p + q - r + 4)}{3} - 3 = 0

\Rightarrow p - q + r - 3 = 0

o r

\Rightarrow x - y + z - 3 = 0

t h i s i s t h e e x p e c t e d r e s u l t .

Commented by rahul 19 last updated on 13/Oct/18

Thank you so much sir !

�� In the formula you posted , if we need to find foot of perpendicular then this factor 2 will not come . right?

Commented by MrW3 last updated on 13/Oct/18

y e s s i r .

f o o t p o i n t (U^{'}, V^{'}, W^{'})

U^{'} = \frac{X + U}{2} = \frac{X}{2} + \frac{X}{2} - \frac{a (a X + b Y + c Z + d)}{a^{2} + b^{2} + c^{2}}

\Rightarrow U^{'} = X - \frac{a (a X + b Y + c Z + d)}{a^{2} + b^{2} + c^{2}}

Commented by MrW3 last updated on 13/Oct/18

t h i s f o r m u l a i s e a s y t o r e m e m b e r

a n d b e u s e d f o r e x a m p l e

t o f i n d t h e d i s t a n c e o f p o i n t (X, Y, Z) t o

a p l a n e :

d = \sqrt{{(X - U^{'})}^{2} + {(Y - V^{'})}^{2} + {(Z - W^{'})}^{2}}

= \frac{∣ a X + b Y + c Z + d ∣}{a^{2} + b^{2} + c^{2}} \sqrt{a^{2} + b^{2} + c^{2}}

= \frac{∣ a X + b Y + c Z + d ∣}{\sqrt{a^{2} + b^{2} + c^{2}}}

Commented by rahul 19 last updated on 13/Oct/18

o k s i r .