Question Number 150121 by mathdanisur last updated on 09/Aug/21
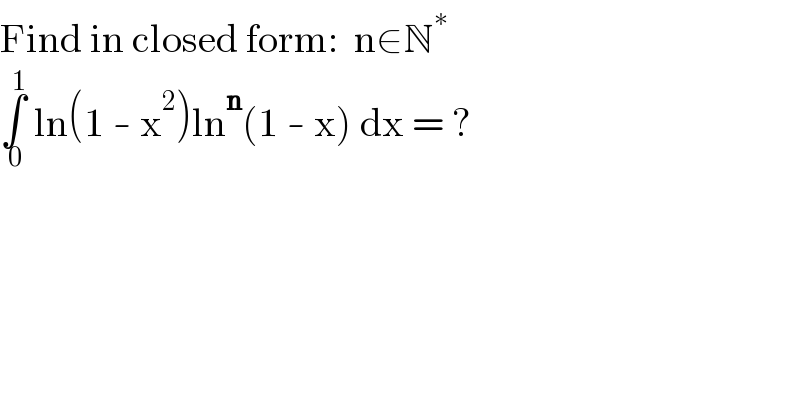
$$\mathrm{Find}\:\mathrm{in}\:\mathrm{closed}\:\mathrm{form}:\:\:\mathrm{n}\in\mathbb{N}^{\ast} \\ $$$$\underset{\:\mathrm{0}} {\overset{\:\mathrm{1}} {\int}}\:\mathrm{ln}\left(\mathrm{1}\:-\:\mathrm{x}^{\mathrm{2}} \right)\mathrm{ln}^{\boldsymbol{\mathrm{n}}} \left(\mathrm{1}\:-\:\mathrm{x}\right)\:\mathrm{dx}\:=\:? \\ $$
Answered by Kamel last updated on 09/Aug/21
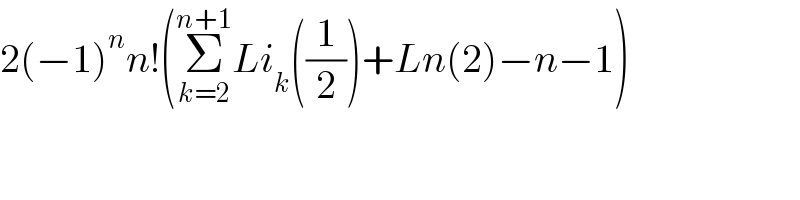
$$\mathrm{2}\left(−\mathrm{1}\right)^{{n}} {n}!\left(\underset{{k}=\mathrm{2}} {\overset{{n}+\mathrm{1}} {\sum}}{Li}_{{k}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)+{Ln}\left(\mathrm{2}\right)−{n}−\mathrm{1}\right) \\ $$
