Question Number 35590 by abdo mathsup 649 cc last updated on 20/May/18
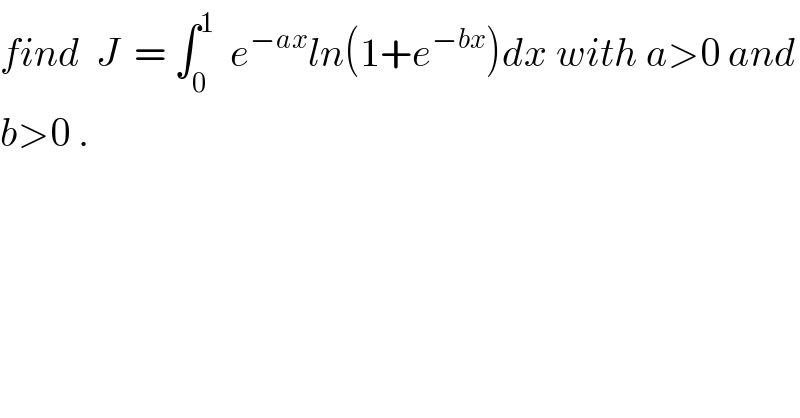
$${find}\:\:{J}\:\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{e}^{−{ax}} {ln}\left(\mathrm{1}+{e}^{−{bx}} \right){dx}\:{with}\:{a}>\mathrm{0}\:{and} \\ $$$${b}>\mathrm{0}\:. \\ $$
