Question Number 29848 by abdo imad last updated on 12/Feb/18
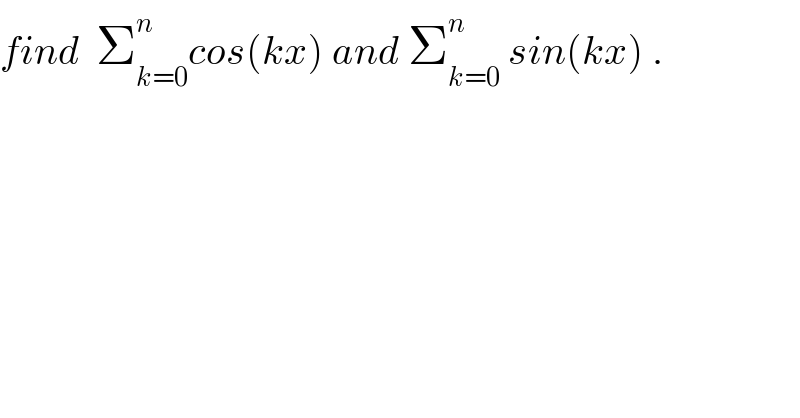
$${find}\:\:\sum_{{k}=\mathrm{0}} ^{{n}} {cos}\left({kx}\right)\:{and}\:\sum_{{k}=\mathrm{0}} ^{{n}} \:{sin}\left({kx}\right)\:. \\ $$
Commented by Tinkutara last updated on 13/Feb/18
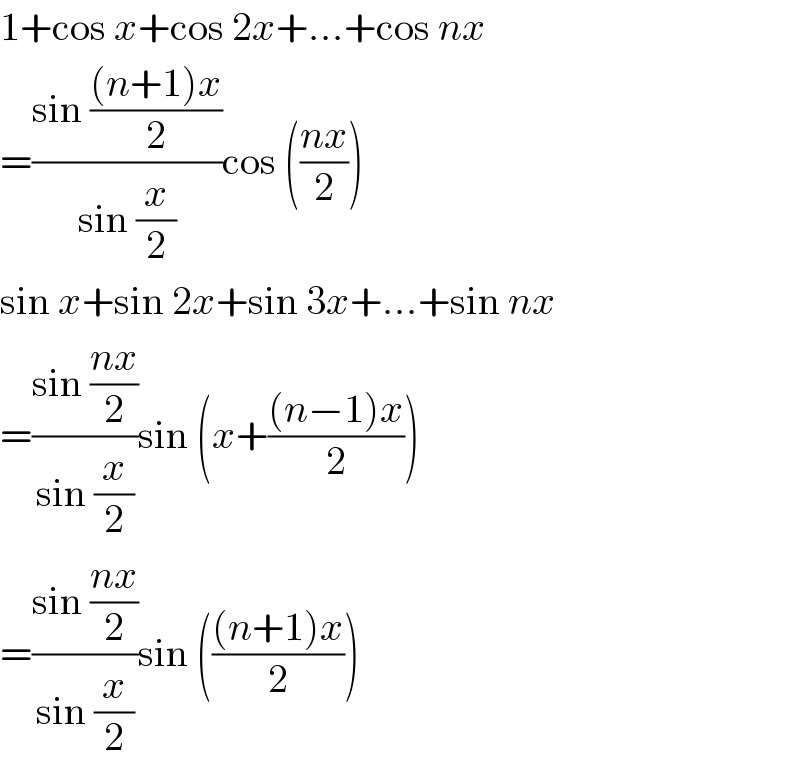
$$\mathrm{1}+\mathrm{cos}\:{x}+\mathrm{cos}\:\mathrm{2}{x}+…+\mathrm{cos}\:{nx} \\ $$$$=\frac{\mathrm{sin}\:\frac{\left({n}+\mathrm{1}\right){x}}{\mathrm{2}}}{\mathrm{sin}\:\frac{{x}}{\mathrm{2}}}\mathrm{cos}\:\left(\frac{{nx}}{\mathrm{2}}\right) \\ $$$$\mathrm{sin}\:{x}+\mathrm{sin}\:\mathrm{2}{x}+\mathrm{sin}\:\mathrm{3}{x}+…+\mathrm{sin}\:{nx} \\ $$$$=\frac{\mathrm{sin}\:\frac{{nx}}{\mathrm{2}}}{\mathrm{sin}\:\frac{{x}}{\mathrm{2}}}\mathrm{sin}\:\left({x}+\frac{\left({n}−\mathrm{1}\right){x}}{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{sin}\:\frac{{nx}}{\mathrm{2}}}{\mathrm{sin}\:\frac{{x}}{\mathrm{2}}}\mathrm{sin}\:\left(\frac{\left({n}+\mathrm{1}\right){x}}{\mathrm{2}}\right) \\ $$
