Question Number 33072 by prof Abdo imad last updated on 10/Apr/18
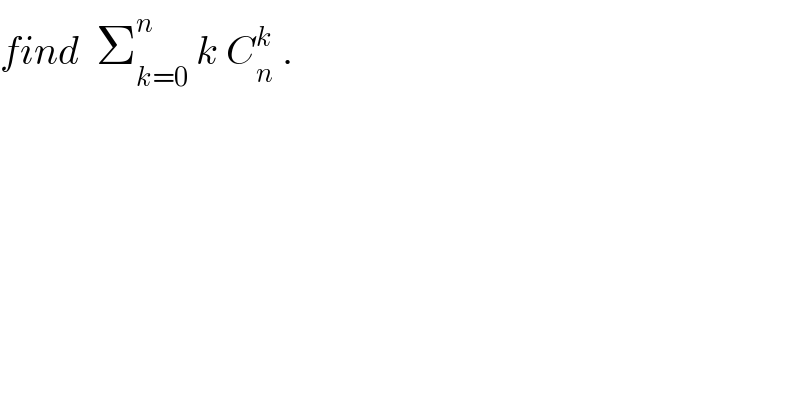
$${find}\:\:\sum_{{k}=\mathrm{0}} ^{{n}} \:{k}\:{C}_{{n}} ^{{k}} \:. \\ $$
Commented by abdo imad last updated on 10/Apr/18
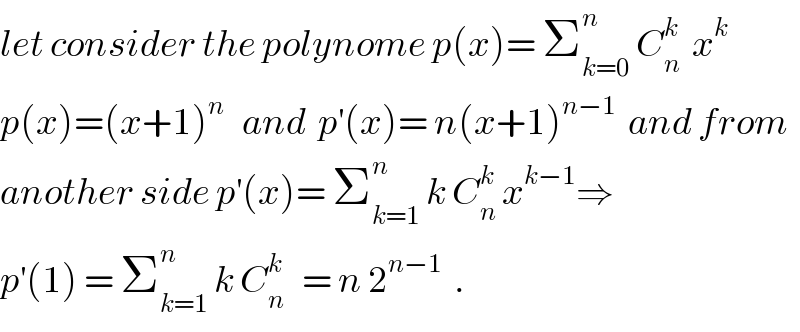
$${let}\:{consider}\:{the}\:{polynome}\:{p}\left({x}\right)=\:\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:\:{x}^{{k}} \\ $$$${p}\left({x}\right)=\left({x}+\mathrm{1}\right)^{{n}} \:\:\:{and}\:\:{p}^{'} \left({x}\right)=\:{n}\left({x}+\mathrm{1}\right)^{{n}−\mathrm{1}} \:\:{and}\:{from} \\ $$$${another}\:{side}\:{p}^{'} \left({x}\right)=\:\sum_{{k}=\mathrm{1}} ^{{n}} \:{k}\:{C}_{{n}} ^{{k}} \:{x}^{{k}−\mathrm{1}} \Rightarrow \\ $$$${p}^{'} \left(\mathrm{1}\right)\:=\:\sum_{{k}=\mathrm{1}} ^{{n}} \:{k}\:{C}_{{n}} ^{{k}} \:\:\:=\:{n}\:\mathrm{2}^{{n}−\mathrm{1}} \:\:. \\ $$
Answered by sma3l2996 last updated on 10/Apr/18
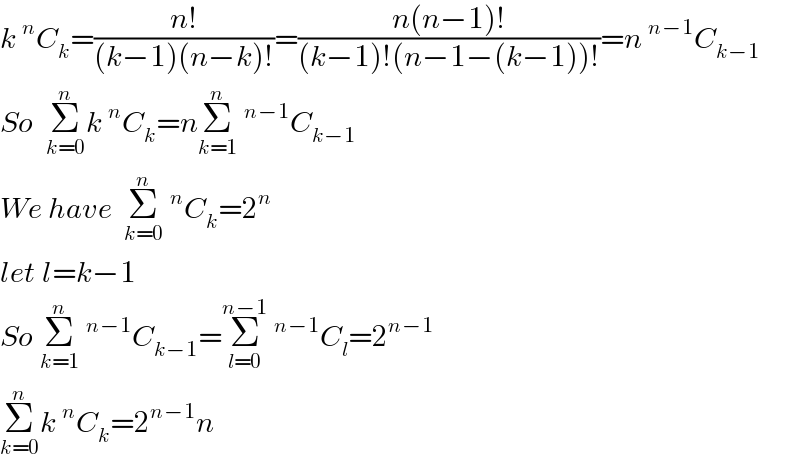
$${k}\:^{{n}} {C}_{{k}} =\frac{{n}!}{\left({k}−\mathrm{1}\right)\left({n}−{k}\right)!}=\frac{{n}\left({n}−\mathrm{1}\right)!}{\left({k}−\mathrm{1}\right)!\left({n}−\mathrm{1}−\left({k}−\mathrm{1}\right)\right)!}={n}\:^{{n}−\mathrm{1}} {C}_{{k}−\mathrm{1}} \\ $$$${So}\:\:\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{k}\:^{{n}} {C}_{{k}} ={n}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\:^{{n}−\mathrm{1}} {C}_{{k}−\mathrm{1}} \\ $$$${We}\:{have}\:\:\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\:^{{n}} {C}_{{k}} =\mathrm{2}^{{n}} \\ $$$${let}\:{l}={k}−\mathrm{1} \\ $$$${So}\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\:^{{n}−\mathrm{1}} {C}_{{k}−\mathrm{1}} =\underset{{l}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\:^{{n}−\mathrm{1}} {C}_{{l}} =\mathrm{2}^{{n}−\mathrm{1}} \: \\ $$$$\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{k}\:^{{n}} {C}_{{k}} =\mathrm{2}^{{n}−\mathrm{1}} {n}\: \\ $$
