Question Number 37365 by math khazana by abdo last updated on 12/Jun/18
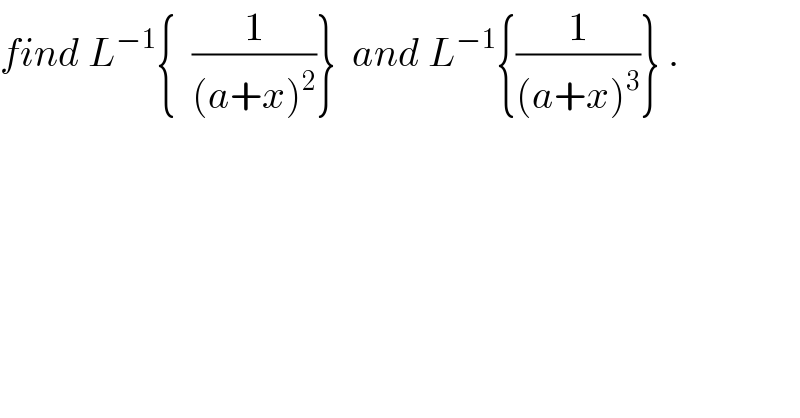
$${find}\:{L}^{−\mathrm{1}} \left\{\:\:\frac{\mathrm{1}}{\left({a}+{x}\right)^{\mathrm{2}} }\right\}\:\:{and}\:{L}^{−\mathrm{1}} \left\{\frac{\mathrm{1}}{\left({a}+{x}\right)^{\mathrm{3}} }\right\}\:. \\ $$
Commented by prof Abdo imad last updated on 15/Jun/18
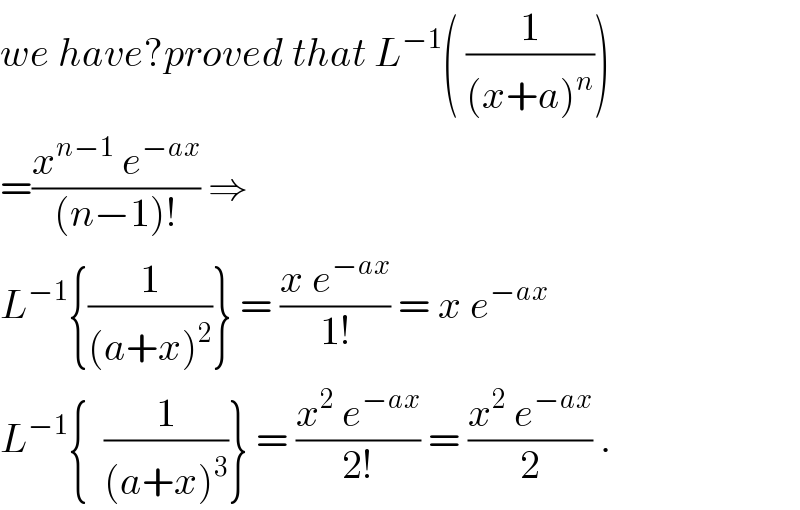
$${we}\:{have}?{proved}\:{that}\:{L}^{−\mathrm{1}} \left(\:\frac{\mathrm{1}}{\left({x}+{a}\right)^{{n}} }\right) \\ $$$$=\frac{{x}^{{n}−\mathrm{1}} \:{e}^{−{ax}} }{\left({n}−\mathrm{1}\right)!}\:\Rightarrow \\ $$$${L}^{−\mathrm{1}} \left\{\frac{\mathrm{1}}{\left({a}+{x}\right)^{\mathrm{2}} }\right\}\:=\:\frac{{x}\:{e}^{−{ax}} }{\mathrm{1}!}\:=\:{x}\:{e}^{−{ax}} \\ $$$${L}^{−\mathrm{1}} \left\{\:\:\frac{\mathrm{1}}{\left({a}+{x}\right)^{\mathrm{3}} }\right\}\:=\:\frac{{x}^{\mathrm{2}} \:{e}^{−{ax}} }{\mathrm{2}!}\:=\:\frac{{x}^{\mathrm{2}} \:{e}^{−{ax}} }{\mathrm{2}}\:. \\ $$
