Question Number 37362 by math khazana by abdo last updated on 12/Jun/18
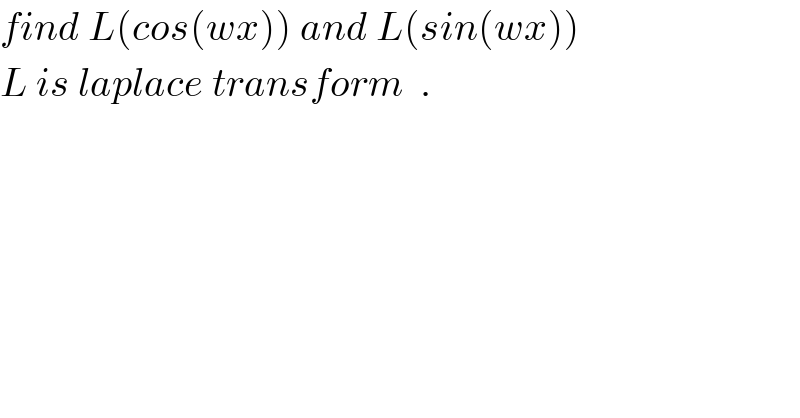
$${find}\:{L}\left({cos}\left({wx}\right)\right)\:{and}\:{L}\left({sin}\left({wx}\right)\right) \\ $$$${L}\:{is}\:{laplace}\:{transform}\:\:. \\ $$
Commented by math khazana by abdo last updated on 13/Jun/18
![L(cos(wx)) =∫_0 ^∞ cos(wt) e^(−xt) dt =Re(∫_0 ^∞ e^(iwt−xt) dt) but ∫_0 ^∞ e^(iwt−xt) dt = ∫_0 ^∞ e^((iw−x)t) dt =(1/(iw−x))[ e^((iw−x)t) ]_(t=0) ^∞ = ((−1)/(iw−x)) = (1/(x−iw)) = ((x+iw)/(x^2 +w^2 )) ⇒ L(cos(wx))= (x/(x^2 +w^2 )) L(si(wx)) =∫_0 ^∞ sin(wt)e^(−xt) dt =Im(∫_0 ^∞ e^(iwt −xt) dt) = (w/(x^2 +w^2 )) ⇒ L(sin(wx)) =(w/(x^2 +w^2 )) .](https://www.tinkutara.com/question/Q37483.png)
$${L}\left({cos}\left({wx}\right)\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:{cos}\left({wt}\right)\:{e}^{−{xt}} {dt}\: \\ $$$$={Re}\left(\int_{\mathrm{0}} ^{\infty} \:\:{e}^{{iwt}−{xt}} {dt}\right)\:{but} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:{e}^{{iwt}−{xt}} {dt}\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:{e}^{\left({iw}−{x}\right){t}} {dt} \\ $$$$=\frac{\mathrm{1}}{{iw}−{x}}\left[\:\:{e}^{\left({iw}−{x}\right){t}} \right]_{{t}=\mathrm{0}} ^{\infty} \:=\:\frac{−\mathrm{1}}{{iw}−{x}}\:=\:\frac{\mathrm{1}}{{x}−{iw}} \\ $$$$=\:\frac{{x}+{iw}}{{x}^{\mathrm{2}} \:+{w}^{\mathrm{2}} }\:\:\:\Rightarrow\:{L}\left({cos}\left({wx}\right)\right)=\:\frac{{x}}{{x}^{\mathrm{2}} \:+{w}^{\mathrm{2}} } \\ $$$${L}\left({si}\left({wx}\right)\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:{sin}\left({wt}\right){e}^{−{xt}} {dt} \\ $$$$={Im}\left(\int_{\mathrm{0}} ^{\infty} \:\:{e}^{{iwt}\:−{xt}} {dt}\right)\:\:=\:\frac{{w}}{{x}^{\mathrm{2}} \:+{w}^{\mathrm{2}} }\:\Rightarrow \\ $$$${L}\left({sin}\left({wx}\right)\right)\:=\frac{{w}}{{x}^{\mathrm{2}} \:+{w}^{\mathrm{2}} }\:. \\ $$
