Question Number 96659 by mathmax by abdo last updated on 03/Jun/20
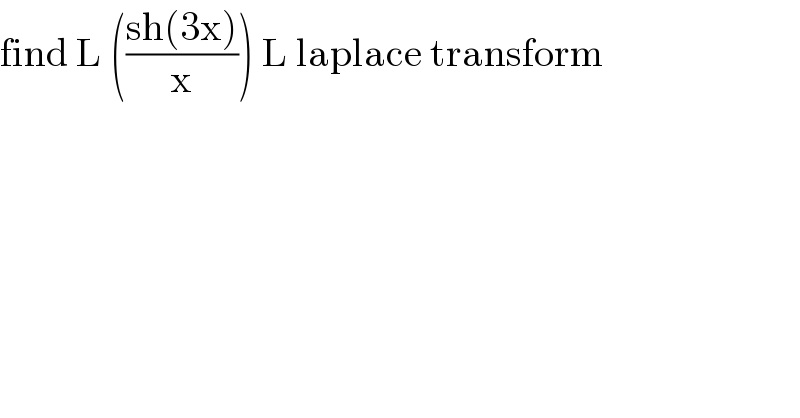
$$\mathrm{find}\:\mathrm{L}\:\left(\frac{\mathrm{sh}\left(\mathrm{3x}\right)}{\mathrm{x}}\right)\:\mathrm{L}\:\mathrm{laplace}\:\mathrm{transform} \\ $$
Answered by Sourav mridha last updated on 07/Jun/20
![f(a)=∫_0 ^∞ e^(−ax) sh(3x)dx =(3/(a^2 −9)) now L[((sh(3x))/x)]=∫_s ^∞ f(a)da =∫_s ^∞ (3/(a^2 −3^2 ))da =(1/2)[ln(((a−3)/(a+3)))]_s ^∞ =ln[((s+3)/(s−3))]^(1/2) ..](https://www.tinkutara.com/question/Q97256.png)
$$\boldsymbol{{f}}\left(\boldsymbol{{a}}\right)=\int_{\mathrm{0}} ^{\infty} \boldsymbol{{e}}^{−\boldsymbol{{ax}}} \boldsymbol{{sh}}\left(\mathrm{3}\boldsymbol{{x}}\right)\boldsymbol{{dx}} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{3}}{\boldsymbol{{a}}^{\mathrm{2}} −\mathrm{9}} \\ $$$$\boldsymbol{{now}}\:\boldsymbol{{L}}\left[\frac{\boldsymbol{{sh}}\left(\mathrm{3}\boldsymbol{{x}}\right)}{\boldsymbol{{x}}}\right]=\int_{\boldsymbol{{s}}} ^{\infty} \boldsymbol{{f}}\left(\boldsymbol{{a}}\right)\boldsymbol{{da}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\int_{\boldsymbol{{s}}} ^{\infty} \frac{\mathrm{3}}{\boldsymbol{{a}}^{\mathrm{2}} −\mathrm{3}^{\mathrm{2}} }\boldsymbol{{da}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left[\boldsymbol{{ln}}\left(\frac{\boldsymbol{{a}}−\mathrm{3}}{\boldsymbol{{a}}+\mathrm{3}}\right)\right]_{\boldsymbol{{s}}} ^{\infty} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\boldsymbol{{ln}}\left[\frac{\boldsymbol{{s}}+\mathrm{3}}{\boldsymbol{{s}}−\mathrm{3}}\right]^{\frac{\mathrm{1}}{\mathrm{2}}} .. \\ $$
