Question Number 146975 by tabata last updated on 16/Jul/21
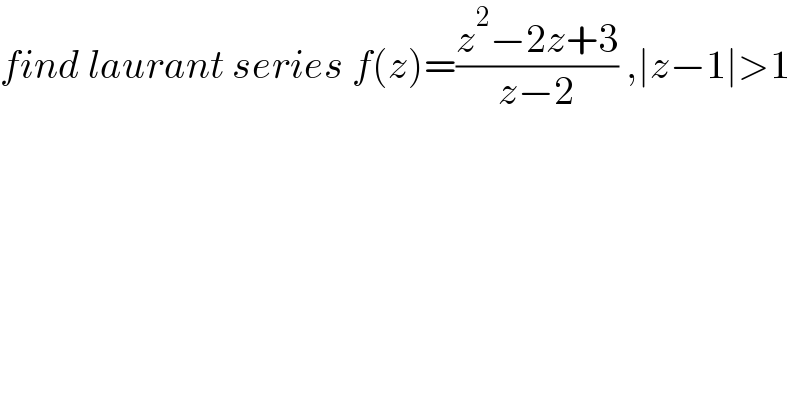
$${find}\:{laurant}\:{series}\:{f}\left({z}\right)=\frac{{z}^{\mathrm{2}} −\mathrm{2}{z}+\mathrm{3}}{{z}−\mathrm{2}}\:,\mid{z}−\mathrm{1}\mid>\mathrm{1} \\ $$
Answered by mathmax by abdo last updated on 17/Jul/21

$$\mathrm{f}\left(\mathrm{z}\right)=\frac{\mathrm{z}^{\mathrm{2}} −\mathrm{2z}+\mathrm{3}}{\mathrm{z}−\mathrm{2}}=\frac{\mathrm{z}^{\mathrm{2}} −\mathrm{2z}}{\mathrm{z}−\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{z}−\mathrm{2}}=\mathrm{z}\:+\frac{\mathrm{3}}{\mathrm{z}−\mathrm{2}} \\ $$$$=\mathrm{z}+\frac{\mathrm{3}}{\mathrm{z}−\mathrm{1}−\mathrm{1}}=\mathrm{z}\:−\frac{\mathrm{3}}{\left(\mathrm{z}−\mathrm{1}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{z}−\mathrm{1}}\right)}\:\:\left(\mid\mathrm{z}−\mathrm{1}\mid>\mathrm{1}\:\Rightarrow\mid\frac{\mathrm{1}}{\mathrm{z}−\mathrm{1}}\mid<\mathrm{1}\right) \\ $$$$=\mathrm{z}−\frac{\mathrm{3}}{\mathrm{z}−\mathrm{1}}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(\frac{\mathrm{1}}{\mathrm{z}−\mathrm{1}}\right)^{\mathrm{n}} \:=\mathrm{z}−\mathrm{3}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{z}−\mathrm{1}\right)^{\mathrm{n}+\mathrm{1}} } \\ $$$$=\mathrm{z}−\mathrm{3}\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{z}−\mathrm{1}\right)^{\mathrm{n}} } \\ $$$$=\mathrm{z}−\mathrm{3}\left(\frac{\mathrm{1}}{\mathrm{z}−\mathrm{1}}+\frac{\mathrm{1}}{\left(\mathrm{z}−\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left(\mathrm{z}−\mathrm{1}\right)^{\mathrm{3}} }+….\right) \\ $$
Commented by mathmax by abdo last updated on 17/Jul/21

$$\mathrm{sorry}\:\mathrm{f}\left(\mathrm{z}\right)=\mathrm{z}+\frac{\mathrm{3}}{\left(\mathrm{z}−\mathrm{1}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{z}−\mathrm{1}}\right)}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{z}\right)=\mathrm{z}+\mathrm{3}\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{z}−\mathrm{1}\right)^{\mathrm{n}} } \\ $$
