Menu Close

find-laurant-series-lf-1-f-z-1-z-1-1-z-2-z-gt-1-2-f-z-1-z-2-2-z-3-z-lt-3-

Tinku Tara 0 Comments
Pin




Question Number 147066 by tabata last updated on 17/Jul/21
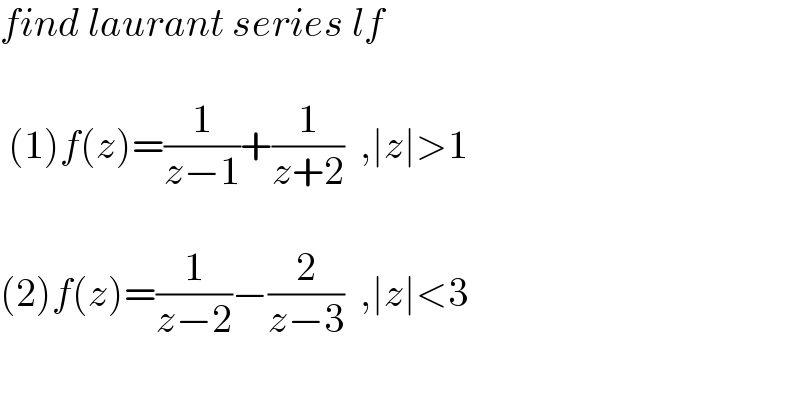
find laurant series lf (1)f(z)=(1/(z−1))+(1/(z+2)) ,∣z∣>1 (2)f(z)=(1/(z−2))−(2/(z−3)) ,∣z∣<3
$${find}\:{laurant}\:{series}\:{lf} \\ $$$$ \\ $$$$\:\left(\mathrm{1}\right){f}\left({z}\right)=\frac{\mathrm{1}}{{z}−\mathrm{1}}+\frac{\mathrm{1}}{{z}+\mathrm{2}}\:\:,\mid{z}\mid>\mathrm{1} \\ $$$$ \\ $$$$\left(\mathrm{2}\right){f}\left({z}\right)=\frac{\mathrm{1}}{{z}−\mathrm{2}}−\frac{\mathrm{2}}{{z}−\mathrm{3}}\:\:,\mid{z}\mid<\mathrm{3} \\ $$
Answered by mathmax by abdo last updated on 17/Jul/21
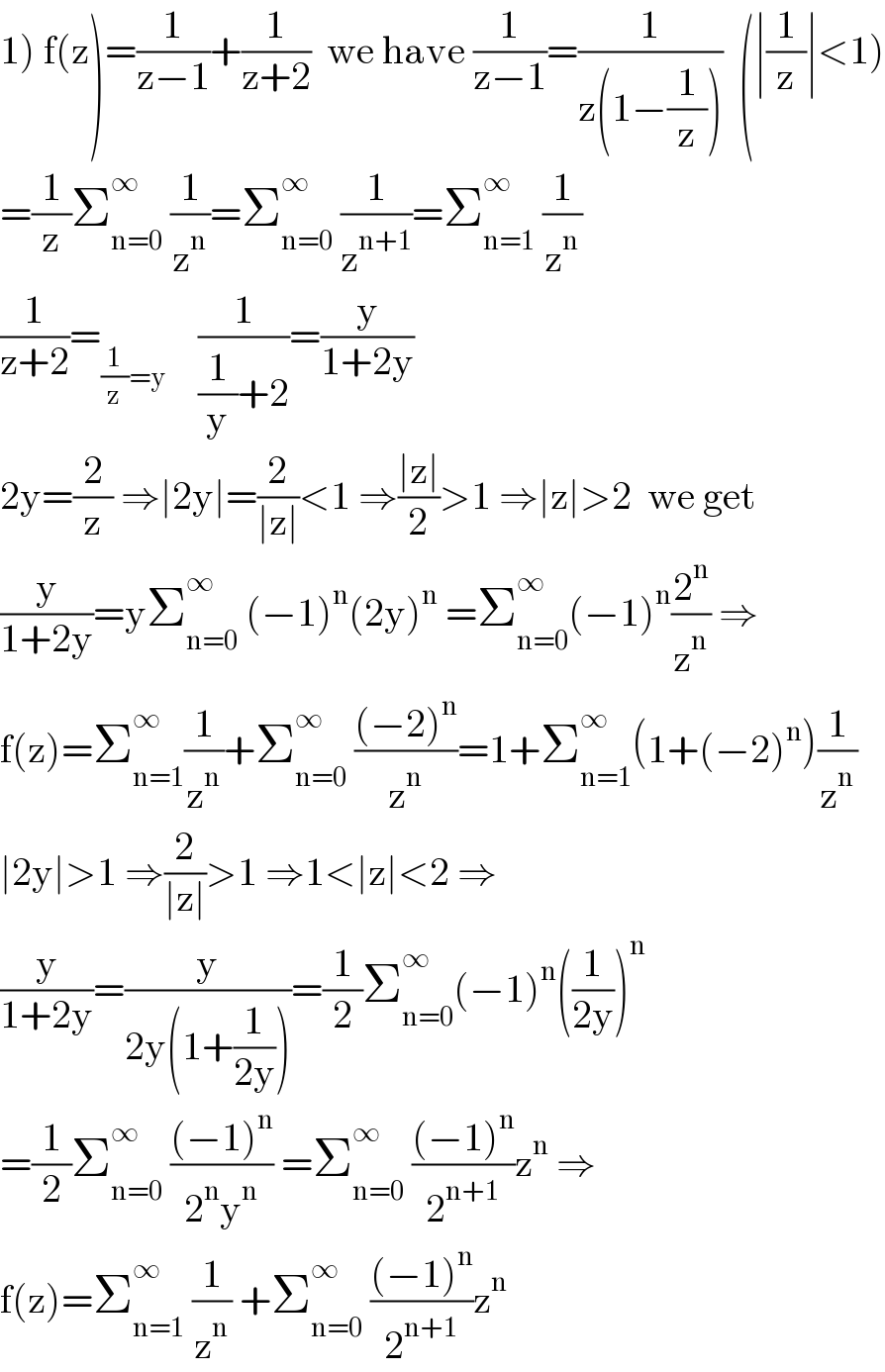
1) f(z)=(1/(z−1))+(1/(z+2)) we have (1/(z−1))=(1/(z(1−(1/z)))) (∣(1/z)∣<1) =(1/z)Σ_(n=0) ^(∞ ) (1/z^n )=Σ_(n=0) ^∞ (1/z^(n+1) )=Σ_(n=1) ^∞ (1/z^n ) (1/(z+2))=_((1/z)=y) (1/((1/y)+2))=(y/(1+2y)) 2y=(2/z) ⇒∣2y∣=(2/(∣z∣))<1 ⇒((∣z∣)/2)>1 ⇒∣z∣>2 we get (y/(1+2y))=yΣ_(n=0) ^∞ (−1)^n (2y)^n =Σ_(n=0) ^∞ (−1)^n (2^n /z^n ) ⇒ f(z)=Σ_(n=1) ^∞ (1/z^n )+Σ_(n=0) ^∞ (((−2)^n )/z^n )=1+Σ_(n=1) ^∞ (1+(−2)^n )(1/z^n ) ∣2y∣>1 ⇒(2/(∣z∣))>1 ⇒1<∣z∣<2 ⇒ (y/(1+2y))=(y/(2y(1+(1/(2y)))))=(1/2)Σ_(n=0) ^∞ (−1)^n ((1/(2y)))^n =(1/2)Σ_(n=0) ^∞ (((−1)^n )/(2^n y^n )) =Σ_(n=0) ^∞ (((−1)^n )/2^(n+1) )z^n ⇒ f(z)=Σ_(n=1) ^∞ (1/z^n ) +Σ_(n=0) ^∞ (((−1)^n )/2^(n+1) )z^n
$$\left.\mathrm{1}\right)\:\mathrm{f}\left(\mathrm{z}\right)=\frac{\mathrm{1}}{\mathrm{z}−\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{z}+\mathrm{2}}\:\:\mathrm{we}\:\mathrm{have}\:\frac{\mathrm{1}}{\mathrm{z}−\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{z}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{z}}\right)}\:\:\left(\mid\frac{\mathrm{1}}{\mathrm{z}}\mid<\mathrm{1}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{z}}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty\:} \:\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{n}} }=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{n}+\mathrm{1}} }=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{n}} } \\ $$$$\frac{\mathrm{1}}{\mathrm{z}+\mathrm{2}}=_{\frac{\mathrm{1}}{\mathrm{z}}=\mathrm{y}} \:\:\:\:\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{y}}+\mathrm{2}}=\frac{\mathrm{y}}{\mathrm{1}+\mathrm{2y}} \\ $$$$\mathrm{2y}=\frac{\mathrm{2}}{\mathrm{z}}\:\Rightarrow\mid\mathrm{2y}\mid=\frac{\mathrm{2}}{\mid\mathrm{z}\mid}<\mathrm{1}\:\Rightarrow\frac{\mid\mathrm{z}\mid}{\mathrm{2}}>\mathrm{1}\:\Rightarrow\mid\mathrm{z}\mid>\mathrm{2}\:\:\mathrm{we}\:\mathrm{get} \\ $$$$\frac{\mathrm{y}}{\mathrm{1}+\mathrm{2y}}=\mathrm{y}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \left(\mathrm{2y}\right)^{\mathrm{n}} \:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \frac{\mathrm{2}^{\mathrm{n}} }{\mathrm{z}^{\mathrm{n}} }\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{z}\right)=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \frac{\mathrm{1}}{\mathrm{z}^{\mathrm{n}} }+\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{2}\right)^{\mathrm{n}} }{\mathrm{z}^{\mathrm{n}} }=\mathrm{1}+\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \left(\mathrm{1}+\left(−\mathrm{2}\right)^{\mathrm{n}} \right)\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{n}} } \\ $$$$\mid\mathrm{2y}\mid>\mathrm{1}\:\Rightarrow\frac{\mathrm{2}}{\mid\mathrm{z}\mid}>\mathrm{1}\:\Rightarrow\mathrm{1}<\mid\mathrm{z}\mid<\mathrm{2}\:\Rightarrow \\ $$$$\frac{\mathrm{y}}{\mathrm{1}+\mathrm{2y}}=\frac{\mathrm{y}}{\mathrm{2y}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2y}}\right)}=\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \left(\frac{\mathrm{1}}{\mathrm{2y}}\right)^{\mathrm{n}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{2}^{\mathrm{n}} \mathrm{y}^{\mathrm{n}} }\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{2}^{\mathrm{n}+\mathrm{1}} }\mathrm{z}^{\mathrm{n}} \:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{z}\right)=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{n}} }\:+\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{2}^{\mathrm{n}+\mathrm{1}} }\mathrm{z}^{\mathrm{n}} \\ $$
Answered by Olaf_Thorendsen last updated on 17/Jul/21
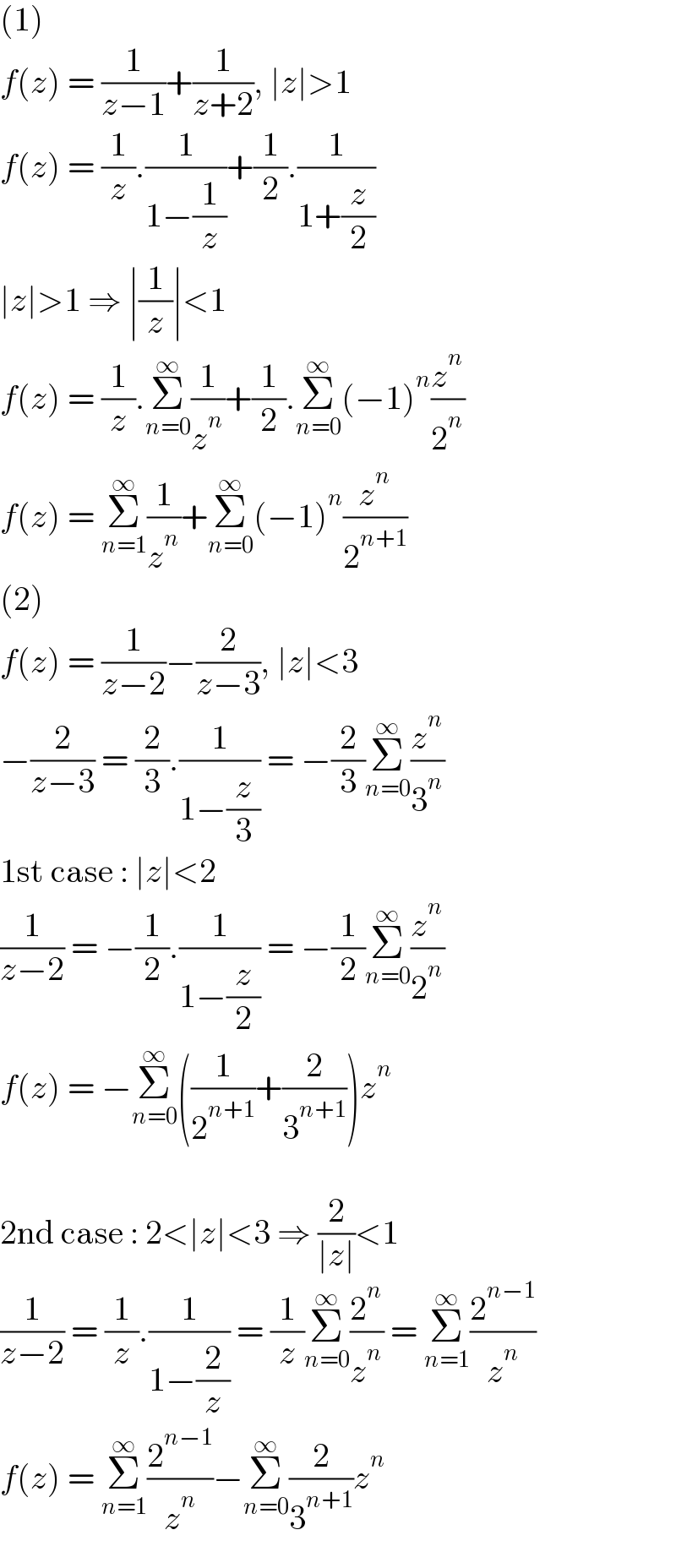
(1) f(z) = (1/(z−1))+(1/(z+2)), ∣z∣>1 f(z) = (1/z).(1/(1−(1/z)))+(1/2).(1/(1+(z/2))) ∣z∣>1 ⇒ ∣(1/z)∣<1 f(z) = (1/z).Σ_(n=0) ^∞ (1/z^n )+(1/2).Σ_(n=0) ^∞ (−1)^n (z^n /2^n ) f(z) = Σ_(n=1) ^∞ (1/z^n )+Σ_(n=0) ^∞ (−1)^n (z^n /2^(n+1) ) (2) f(z) = (1/(z−2))−(2/(z−3)), ∣z∣<3 −(2/(z−3)) = (2/3).(1/(1−(z/3))) = −(2/3)Σ_(n=0) ^∞ (z^n /3^n ) 1st case : ∣z∣<2 (1/(z−2)) = −(1/2).(1/(1−(z/2))) = −(1/2)Σ_(n=0) ^∞ (z^n /2^n ) f(z) = −Σ_(n=0) ^∞ ((1/2^(n+1) )+(2/3^(n+1) ))z^n 2nd case : 2<∣z∣<3 ⇒ (2/(∣z∣))<1 (1/(z−2)) = (1/z).(1/(1−(2/z))) = (1/z)Σ_(n=0) ^∞ (2^n /z^n ) = Σ_(n=1) ^∞ (2^(n−1) /z^n ) f(z) = Σ_(n=1) ^∞ (2^(n−1) /z^n )−Σ_(n=0) ^∞ (2/3^(n+1) )z^n
$$\left(\mathrm{1}\right) \\ $$$${f}\left({z}\right)\:=\:\frac{\mathrm{1}}{{z}−\mathrm{1}}+\frac{\mathrm{1}}{{z}+\mathrm{2}},\:\mid{z}\mid>\mathrm{1} \\ $$$${f}\left({z}\right)\:=\:\frac{\mathrm{1}}{{z}}.\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{{z}}}+\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{1}}{\mathrm{1}+\frac{{z}}{\mathrm{2}}} \\ $$$$\mid{z}\mid>\mathrm{1}\:\Rightarrow\:\mid\frac{\mathrm{1}}{{z}}\mid<\mathrm{1} \\ $$$${f}\left({z}\right)\:=\:\frac{\mathrm{1}}{{z}}.\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{z}^{{n}} }+\frac{\mathrm{1}}{\mathrm{2}}.\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \frac{{z}^{{n}} }{\mathrm{2}^{{n}} } \\ $$$${f}\left({z}\right)\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{z}^{{n}} }+\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \frac{{z}^{{n}} }{\mathrm{2}^{{n}+\mathrm{1}} } \\ $$$$\left(\mathrm{2}\right) \\ $$$${f}\left({z}\right)\:=\:\frac{\mathrm{1}}{{z}−\mathrm{2}}−\frac{\mathrm{2}}{{z}−\mathrm{3}},\:\mid{z}\mid<\mathrm{3} \\ $$$$−\frac{\mathrm{2}}{{z}−\mathrm{3}}\:=\:\frac{\mathrm{2}}{\mathrm{3}}.\frac{\mathrm{1}}{\mathrm{1}−\frac{{z}}{\mathrm{3}}}\:=\:−\frac{\mathrm{2}}{\mathrm{3}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{z}^{{n}} }{\mathrm{3}^{{n}} } \\ $$$$\mathrm{1st}\:\mathrm{case}\::\:\mid{z}\mid<\mathrm{2} \\ $$$$\frac{\mathrm{1}}{{z}−\mathrm{2}}\:=\:−\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{1}}{\mathrm{1}−\frac{{z}}{\mathrm{2}}}\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{z}^{{n}} }{\mathrm{2}^{{n}} } \\ $$$${f}\left({z}\right)\:=\:−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{2}^{{n}+\mathrm{1}} }+\frac{\mathrm{2}}{\mathrm{3}^{{n}+\mathrm{1}} }\right){z}^{{n}} \\ $$$$ \\ $$$$\mathrm{2nd}\:\mathrm{case}\::\:\mathrm{2}<\mid{z}\mid<\mathrm{3}\:\Rightarrow\:\frac{\mathrm{2}}{\mid{z}\mid}<\mathrm{1} \\ $$$$\frac{\mathrm{1}}{{z}−\mathrm{2}}\:=\:\frac{\mathrm{1}}{{z}}.\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{2}}{{z}}}\:=\:\frac{\mathrm{1}}{{z}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{2}^{{n}} }{{z}^{{n}} }\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{2}^{{n}−\mathrm{1}} }{{z}^{{n}} } \\ $$$${f}\left({z}\right)\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{2}^{{n}−\mathrm{1}} }{{z}^{{n}} }−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{2}}{\mathrm{3}^{{n}+\mathrm{1}} }{z}^{{n}} \\ $$
Commented by Mrsof last updated on 17/Jul/21
sir why you give ∣z∣<2 ?
$${sir}\:{why}\:{you}\:{give}\:\mid{z}\mid<\mathrm{2}\:? \\ $$
Commented by Olaf_Thorendsen last updated on 17/Jul/21
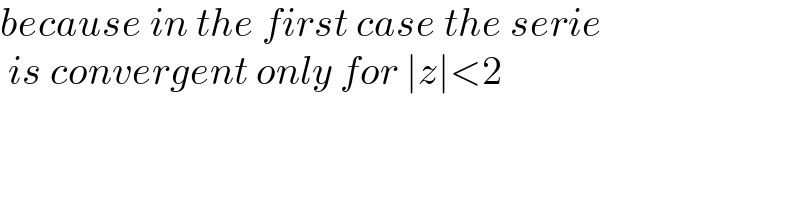
because in the first case the serie is convergent only for ∣z∣<2
$${because}\:{in}\:{the}\:{first}\:{case}\:{the}\:{serie} \\ $$$$\:{is}\:{convergent}\:{only}\:{for}\:\mid{z}\mid<\mathrm{2} \\ $$
Commented by Mrsof last updated on 18/Jul/21
thank you sir
$${thank}\:{you}\:{sir} \\ $$
Answered by mathmax by abdo last updated on 17/Jul/21
2)g(z)=(1/(z−2))−(2/(z−3)) we have (2/(z−3))=−(2/(3−z))=((−2)/(3(1−(z/3))))=−(2/3)Σ_(n=0) ^∞ (z^n /3^n )=−2Σ_(n=0) ^∞ (z^n /3^(n+1) ) (∣(z/3)∣<1) (1/(z−2))=_(y=(z/3)) (1/(3y−2)) =((−1)/(2−3y)) =((−1)/(2(1−(3/2)y))) ∣((3y)/2)∣=∣(z/2)∣<1 ⇒∣z∣<2 inthis case we get (1/(z−2))=−(1/2)Σ_(n=0) ^∞ ((3/2))^n y^n =−(1/2)Σ_(n=0) ^∞ (3^n /2^n )(z^n /3^n )=−(1/2)Σ_(n=0) ^∞ (z^n /2^n ) ⇒ g(z)=−2Σ_(n=0) ^∞ (z^n /3^(n+1) )−Σ_(n=0) ^∞ (z^n /2^(n+1) )=Σ_(n=0) ^∞ (−(2/3^(n+1) )−(1/2^(n+1) ))z^n ∣((3y)/2)∣>1 ⇒∣(z/2)∣>1 ⇒2<∣z∣<3 we get (1/(z−2))=((−1)/(3y((2/(3y))−1)))=(1/(3y(1−(2/(3y)))))=(1/(3y))Σ_(n=0) ^∞ ((2/(3y)))^n =(1/z)Σ_(n=0) ^∞ (2^n /z^n ) =Σ_(n=0) ^∞ (2^n /z^(n+1) ) ⇒g(z)=−2Σ_(n=0) ^∞ (z^n /3^(n+1) )+Σ_(n=0) ^∞ (2^n /z^(n+1) )
$$\left.\mathrm{2}\right)\mathrm{g}\left(\mathrm{z}\right)=\frac{\mathrm{1}}{\mathrm{z}−\mathrm{2}}−\frac{\mathrm{2}}{\mathrm{z}−\mathrm{3}}\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\frac{\mathrm{2}}{\mathrm{z}−\mathrm{3}}=−\frac{\mathrm{2}}{\mathrm{3}−\mathrm{z}}=\frac{−\mathrm{2}}{\mathrm{3}\left(\mathrm{1}−\frac{\mathrm{z}}{\mathrm{3}}\right)}=−\frac{\mathrm{2}}{\mathrm{3}}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{z}^{\mathrm{n}} }{\mathrm{3}^{\mathrm{n}} }=−\mathrm{2}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{z}^{\mathrm{n}} }{\mathrm{3}^{\mathrm{n}+\mathrm{1}} }\:\:\:\left(\mid\frac{\mathrm{z}}{\mathrm{3}}\mid<\mathrm{1}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{z}−\mathrm{2}}=_{\mathrm{y}=\frac{\mathrm{z}}{\mathrm{3}}} \:\:\frac{\mathrm{1}}{\mathrm{3y}−\mathrm{2}}\:=\frac{−\mathrm{1}}{\mathrm{2}−\mathrm{3y}}\:=\frac{−\mathrm{1}}{\mathrm{2}\left(\mathrm{1}−\frac{\mathrm{3}}{\mathrm{2}}\mathrm{y}\right)} \\ $$$$\mid\frac{\mathrm{3y}}{\mathrm{2}}\mid=\mid\frac{\mathrm{z}}{\mathrm{2}}\mid<\mathrm{1}\:\Rightarrow\mid\mathrm{z}\mid<\mathrm{2}\:\:\mathrm{inthis}\:\mathrm{case}\:\mathrm{we}\:\mathrm{get} \\ $$$$\frac{\mathrm{1}}{\mathrm{z}−\mathrm{2}}=−\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{n}} \mathrm{y}^{\mathrm{n}} \:=−\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \frac{\mathrm{3}^{\mathrm{n}} }{\mathrm{2}^{\mathrm{n}} }\frac{\mathrm{z}^{\mathrm{n}} }{\mathrm{3}^{\mathrm{n}} }=−\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{z}^{\mathrm{n}} }{\mathrm{2}^{\mathrm{n}} }\:\Rightarrow \\ $$$$\mathrm{g}\left(\mathrm{z}\right)=−\mathrm{2}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{z}^{\mathrm{n}} }{\mathrm{3}^{\mathrm{n}+\mathrm{1}} }−\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{z}^{\mathrm{n}} }{\mathrm{2}^{\mathrm{n}+\mathrm{1}} }=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\frac{\mathrm{2}}{\mathrm{3}^{\mathrm{n}+\mathrm{1}} }−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}+\mathrm{1}} }\right)\mathrm{z}^{\mathrm{n}} \\ $$$$\mid\frac{\mathrm{3y}}{\mathrm{2}}\mid>\mathrm{1}\:\Rightarrow\mid\frac{\mathrm{z}}{\mathrm{2}}\mid>\mathrm{1}\:\Rightarrow\mathrm{2}<\mid\mathrm{z}\mid<\mathrm{3}\:\:\mathrm{we}\:\mathrm{get}\: \\ $$$$\frac{\mathrm{1}}{\mathrm{z}−\mathrm{2}}=\frac{−\mathrm{1}}{\mathrm{3y}\left(\frac{\mathrm{2}}{\mathrm{3y}}−\mathrm{1}\right)}=\frac{\mathrm{1}}{\mathrm{3y}\left(\mathrm{1}−\frac{\mathrm{2}}{\mathrm{3y}}\right)}=\frac{\mathrm{1}}{\mathrm{3y}}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(\frac{\mathrm{2}}{\mathrm{3y}}\right)^{\mathrm{n}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{z}}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{2}^{\mathrm{n}} }{\mathrm{z}^{\mathrm{n}} }\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{2}^{\mathrm{n}} }{\mathrm{z}^{\mathrm{n}+\mathrm{1}} }\:\Rightarrow\mathrm{g}\left(\mathrm{z}\right)=−\mathrm{2}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{z}^{\mathrm{n}} }{\mathrm{3}^{\mathrm{n}+\mathrm{1}} }+\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{2}^{\mathrm{n}} }{\mathrm{z}^{\mathrm{n}+\mathrm{1}} } \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *