Menu Close

find-laurent-series-f-z-1-z-2-z-1-0-lt-z-1-lt-1-

Tinku Tara 0 Comments
Pin




Question Number 148724 by Sozan last updated on 30/Jul/21
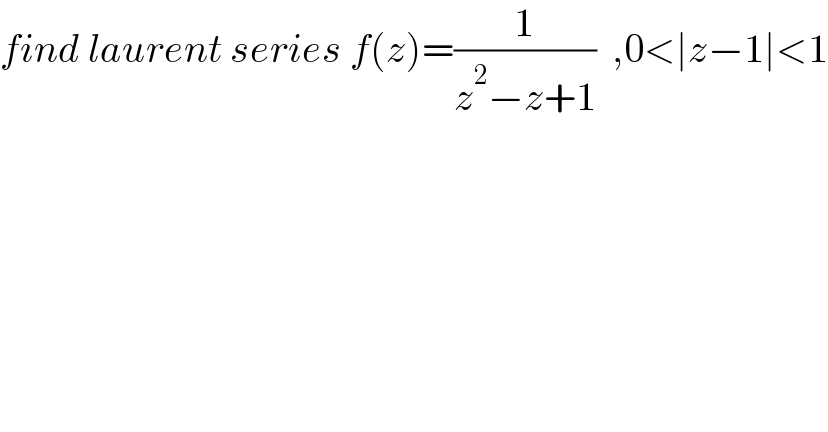
find laurent series f(z)=(1/(z^2 −z+1)) ,0<∣z−1∣<1
$${find}\:{laurent}\:{series}\:{f}\left({z}\right)=\frac{\mathrm{1}}{{z}^{\mathrm{2}} −{z}+\mathrm{1}}\:\:,\mathrm{0}<\mid{z}−\mathrm{1}\mid<\mathrm{1} \\ $$
Answered by mathmax by abdo last updated on 30/Jul/21
the way of this kind is to use changement z−1=y ⇒ f(z)=ϕ(y)=(1/((y+1)^2 −(y+1)+1))=(1/(y^2 +2y+1−y)) =(1/(y^2 +y+1)) roots of y^2 +y+1=0 Δ=1−4=−3 ⇒z_1 =((−1+i(√3))/2)=e^((2iπ)/3) and z_2 =((−1−i(√3))/2)=e^(−((2iπ)/3)) ⇒ϕ(y)=(1/((y−z_1 )(y−z_2 )))=(1/(z_1 −z_2 ))((1/(y−z_1 ))−(1/(y−z_2 ))) =(1/(2i.((√3)/2)))((1/(y−z_1 ))−(1/(y−z_2 ))) we have ∣(y/z_1 )∣=∣y∣<1 ∣(y/z_2 )∣=∣y∣<1 ⇒ϕ(y)=(1/(i(√3))){ (1/(z_1 ((y/z_1 )−1)))−(1/(z_2 ((y/z_2 )−1)))} =(1/(i(√3)))((1/z_2 )×(1/(1−(y/z_2 )))−(1/z_1 )×(1/(1−(y/z_1 )))) =(e^((2iπ)/3) /(i(√3)))Σ_(n=0) ^∞ (y^n /z_2 ^n )−(e^(−((2iπ)/3)) /(i(√3)))Σ_(n=0) ^∞ (y^n /z_1 ^n ) =(1/(i(√3)))e^((2iπ)/3) Σ_(n=0) ^∞ e^((i2nπ)/3) y^n −(1/(i(√3)))e^((−2iπ)/3) Σ_(n=0) ^∞ e^(−((i2nπ)/3)) y^n =(1/(i(√3)))Σ_(n=0) ^∞ e^((i(2n+1)π)/3) (z−1)^n −(1/(i(√3)))Σ_(n=0) ^∞ e^(−((i(2n+1)π)/3)) (z−1)^n =(1/(i(√3)))Σ_(n=0) ^∞ 2isin((((2n+1)π)/3))(z−1)^n ⇒ f(z)=(2/( (√3)))Σ_(n=0) ^∞ sin((((2n+1)π)/3))(z−1)^n
$$\mathrm{the}\:\mathrm{way}\:\mathrm{of}\:\mathrm{this}\:\mathrm{kind}\:\mathrm{is}\:\mathrm{to}\:\mathrm{use}\:\mathrm{changement}\:\mathrm{z}−\mathrm{1}=\mathrm{y}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{z}\right)=\varphi\left(\mathrm{y}\right)=\frac{\mathrm{1}}{\left(\mathrm{y}+\mathrm{1}\right)^{\mathrm{2}} −\left(\mathrm{y}+\mathrm{1}\right)+\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{y}^{\mathrm{2}} \:+\mathrm{2y}+\mathrm{1}−\mathrm{y}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{y}^{\mathrm{2}} +\mathrm{y}+\mathrm{1}}\:\:\:\mathrm{roots}\:\mathrm{of}\:\mathrm{y}^{\mathrm{2}} \:+\mathrm{y}+\mathrm{1}=\mathrm{0} \\ $$$$\Delta=\mathrm{1}−\mathrm{4}=−\mathrm{3}\:\Rightarrow\mathrm{z}_{\mathrm{1}} =\frac{−\mathrm{1}+\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}=\mathrm{e}^{\frac{\mathrm{2i}\pi}{\mathrm{3}}} \:\:\mathrm{and}\:\mathrm{z}_{\mathrm{2}} =\frac{−\mathrm{1}−\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}=\mathrm{e}^{−\frac{\mathrm{2i}\pi}{\mathrm{3}}} \\ $$$$\Rightarrow\varphi\left(\mathrm{y}\right)=\frac{\mathrm{1}}{\left(\mathrm{y}−\mathrm{z}_{\mathrm{1}} \right)\left(\mathrm{y}−\mathrm{z}_{\mathrm{2}} \right)}=\frac{\mathrm{1}}{\mathrm{z}_{\mathrm{1}} −\mathrm{z}_{\mathrm{2}} }\left(\frac{\mathrm{1}}{\mathrm{y}−\mathrm{z}_{\mathrm{1}} }−\frac{\mathrm{1}}{\mathrm{y}−\mathrm{z}_{\mathrm{2}} }\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2i}.\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\left(\frac{\mathrm{1}}{\mathrm{y}−\mathrm{z}_{\mathrm{1}} }−\frac{\mathrm{1}}{\mathrm{y}−\mathrm{z}_{\mathrm{2}} }\right)\:\:\mathrm{we}\:\mathrm{have}\:\mid\frac{\mathrm{y}}{\mathrm{z}_{\mathrm{1}} }\mid=\mid\mathrm{y}\mid<\mathrm{1} \\ $$$$\mid\frac{\mathrm{y}}{\mathrm{z}_{\mathrm{2}} }\mid=\mid\mathrm{y}\mid<\mathrm{1}\:\Rightarrow\varphi\left(\mathrm{y}\right)=\frac{\mathrm{1}}{\mathrm{i}\sqrt{\mathrm{3}}}\left\{\:\:\frac{\mathrm{1}}{\mathrm{z}_{\mathrm{1}} \left(\frac{\mathrm{y}}{\mathrm{z}_{\mathrm{1}} }−\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{z}_{\mathrm{2}} \left(\frac{\mathrm{y}}{\mathrm{z}_{\mathrm{2}} }−\mathrm{1}\right)}\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{i}\sqrt{\mathrm{3}}}\left(\frac{\mathrm{1}}{\mathrm{z}_{\mathrm{2}} }×\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{y}}{\mathrm{z}_{\mathrm{2}} }}−\frac{\mathrm{1}}{\mathrm{z}_{\mathrm{1}} }×\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{y}}{\mathrm{z}_{\mathrm{1}} }}\right) \\ $$$$=\frac{\mathrm{e}^{\frac{\mathrm{2i}\pi}{\mathrm{3}}} }{\mathrm{i}\sqrt{\mathrm{3}}}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{y}^{\mathrm{n}} }{\mathrm{z}_{\mathrm{2}} ^{\mathrm{n}} }−\frac{\mathrm{e}^{−\frac{\mathrm{2i}\pi}{\mathrm{3}}} }{\mathrm{i}\sqrt{\mathrm{3}}}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{y}^{\mathrm{n}} }{\mathrm{z}_{\mathrm{1}} ^{\mathrm{n}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{i}\sqrt{\mathrm{3}}}\mathrm{e}^{\frac{\mathrm{2i}\pi}{\mathrm{3}}} \:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{e}^{\frac{\mathrm{i2n}\pi}{\mathrm{3}}} \:\mathrm{y}^{\mathrm{n}} \:\:−\frac{\mathrm{1}}{\mathrm{i}\sqrt{\mathrm{3}}}\mathrm{e}^{\frac{−\mathrm{2i}\pi}{\mathrm{3}}} \:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\frac{\mathrm{i2n}\pi}{\mathrm{3}}} \:\mathrm{y}^{\mathrm{n}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{i}\sqrt{\mathrm{3}}}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{e}^{\frac{\mathrm{i}\left(\mathrm{2n}+\mathrm{1}\right)\pi}{\mathrm{3}}} \:\left(\mathrm{z}−\mathrm{1}\right)^{\mathrm{n}} \:−\frac{\mathrm{1}}{\mathrm{i}\sqrt{\mathrm{3}}}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\frac{\mathrm{i}\left(\mathrm{2n}+\mathrm{1}\right)\pi}{\mathrm{3}}} \:\left(\mathrm{z}−\mathrm{1}\right)^{\mathrm{n}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{i}\sqrt{\mathrm{3}}}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \mathrm{2isin}\left(\frac{\left(\mathrm{2n}+\mathrm{1}\right)\pi}{\mathrm{3}}\right)\left(\mathrm{z}−\mathrm{1}\right)^{\mathrm{n}} \:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{z}\right)=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{sin}\left(\frac{\left(\mathrm{2n}+\mathrm{1}\right)\pi}{\mathrm{3}}\right)\left(\mathrm{z}−\mathrm{1}\right)^{\mathrm{n}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *