Question Number 177929 by Spillover last updated on 11/Oct/22
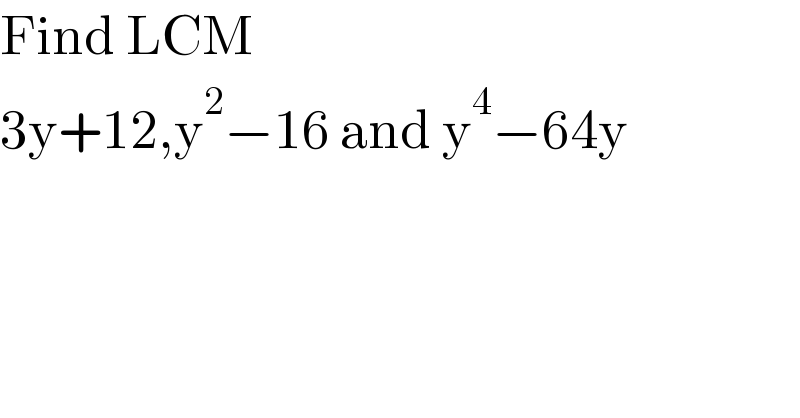
$$\mathrm{Find}\:\mathrm{LCM}\: \\ $$$$\mathrm{3y}+\mathrm{12},\mathrm{y}^{\mathrm{2}} −\mathrm{16}\:\mathrm{and}\:\mathrm{y}^{\mathrm{4}} −\mathrm{64y} \\ $$
Answered by Ar Brandon last updated on 11/Oct/22

$$\mathrm{3y}+\mathrm{12},\:\mathrm{y}^{\mathrm{2}} −\mathrm{16},\:\mathrm{y}^{\mathrm{4}} −\mathrm{64y} \\ $$$$\Leftrightarrow\mathrm{3}\left(\mathrm{y}+\mathrm{4}\right),\:\left(\mathrm{y}−\mathrm{4}\right)\left(\mathrm{y}+\mathrm{4}\right),\:\mathrm{y}\left(\mathrm{y}−\mathrm{4}\right)\left(\mathrm{y}^{\mathrm{2}} +\mathrm{4y}+\mathrm{16}\right) \\ $$$$\begin{array}{|c|c|c|c|c|c|}{\mathrm{y}+\mathrm{4}}&\hline{\mathrm{3}\left(\mathrm{y}+\mathrm{4}\right)}&\hline{\left(\mathrm{y}−\mathrm{4}\right)\left(\mathrm{y}+\mathrm{4}\right)}&\hline{\mathrm{y}\left(\mathrm{y}−\mathrm{4}\right)\left(\mathrm{y}^{\mathrm{2}} +\mathrm{4y}+\mathrm{16}\right)}\\{\mathrm{y}−\mathrm{4}}&\hline{\mathrm{3}}&\hline{\mathrm{y}−\mathrm{4}}&\hline{\mathrm{y}\left(\mathrm{y}−\mathrm{4}\right)\left(\mathrm{y}^{\mathrm{2}} +\mathrm{4y}+\mathrm{16}\right)}\\{\mathrm{y}^{\mathrm{2}} +\mathrm{4y}+\mathrm{16}}&\hline{\mathrm{3}}&\hline{\mathrm{1}}&\hline{\mathrm{y}\left(\mathrm{y}^{\mathrm{2}} +\mathrm{4y}+\mathrm{16}\right)}\\{\mathrm{y}}&\hline{\mathrm{3}}&\hline{\mathrm{1}}&\hline{\mathrm{y}}\\{\mathrm{3}}&\hline{\mathrm{3}}&\hline{\mathrm{1}}&\hline{\mathrm{1}}\\{}&\hline{\mathrm{1}}&\hline{\mathrm{1}}&\hline{\mathrm{1}}\\\hline\end{array} \\ $$$${L}.{C}.{M}=\mathrm{3y}\left(\mathrm{y}−\mathrm{4}\right)\left(\mathrm{y}+\mathrm{4}\right)\left(\mathrm{y}^{\mathrm{2}} +\mathrm{4y}+\mathrm{16}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{3}\left(\mathrm{y}+\mathrm{4}\right)\left(\mathrm{y}^{\mathrm{4}} −\mathrm{64y}\right) \\ $$
Commented by Spillover last updated on 11/Oct/22

$$\mathrm{thank}\:\mathrm{you} \\ $$
