Question Number 39838 by math khazana by abdo last updated on 12/Jul/18
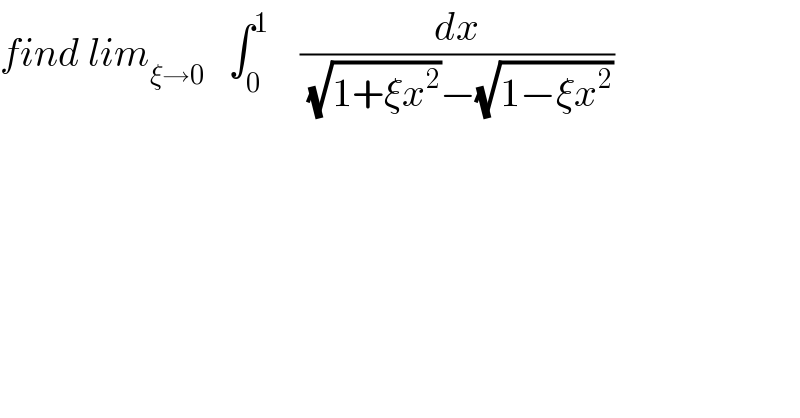
$${find}\:{lim}_{\xi\rightarrow\mathrm{0}} \:\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{{dx}}{\:\sqrt{\mathrm{1}+\xi{x}^{\mathrm{2}} }−\sqrt{\mathrm{1}−\xi{x}^{\mathrm{2}} }}\: \\ $$
Commented by maxmathsup by imad last updated on 24/Jul/18
![let I(ξ) = ∫_0 ^1 (dx/( (√(1+ξx^2 ))−(√(1−ξx^2 )))) I(ξ) = ∫_0 ^1 (((√(1+ξx^2 ))+(√(1−ξx^2 )))/(2ξx^2 )) dx = (1/(2ξ)) ∫_0 ^1 ((√(1+ξx^2 ))/x^2 )dx +(1/(2ξ)) ∫_0 ^1 ((√(1−ξx^2 ))/x^2 ) dx but (√(1+ξx^2 ))=(1+ξx^2 )^(1/2) =1+(1/2)((ξx^2 )/(1!)) (((1/2)((1/2)−1))/(2!)) (ξx^2 )^2 +o(ξ) =1+((ξx^2 )/2) −(1/8) ξ^2 x^4 +o(ξ) ⇒ ((√(1+ξx^2 ))/x^2 ) =(1/x^2 ) +(ξ/2) −(1/8) ξ^2 x^2 +o(ξ) also ((√(1−ξx^2 ))/x^2 ) = (1/x^2 ) −(ξ/2) +(1/8) ξ^2 x^2 +o(ξ) ⇒⇒(((√(1+ξx^2 ))+(√(1−ξx^2 )))/(2ξx^2 )) =(1/(2ξx^2 )){ (2/x^2 ) +o(ξ)} = (1/(ξ x^4 )) +o(ξ) ⇒ I(ξ) ∼ (1/ξ) ∫_0 ^1 (dx/x^4 ) =(1/ξ)[(1/(−4+1)) x^(−4+1) ]_0 ^1 =−(1/(3ξ))[ (1/x^3 )]_0 ^1 =∞](https://www.tinkutara.com/question/Q40578.png)
$${let}\:{I}\left(\xi\right)\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\:\frac{{dx}}{\:\sqrt{\mathrm{1}+\xi{x}^{\mathrm{2}} }−\sqrt{\mathrm{1}−\xi{x}^{\mathrm{2}} }}\: \\ $$$${I}\left(\xi\right)\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\sqrt{\mathrm{1}+\xi{x}^{\mathrm{2}} }+\sqrt{\mathrm{1}−\xi{x}^{\mathrm{2}} }}{\mathrm{2}\xi{x}^{\mathrm{2}} }\:{dx} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}\xi}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{\sqrt{\mathrm{1}+\xi{x}^{\mathrm{2}} }}{{x}^{\mathrm{2}} }{dx}\:+\frac{\mathrm{1}}{\mathrm{2}\xi}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{\sqrt{\mathrm{1}−\xi{x}^{\mathrm{2}} }}{{x}^{\mathrm{2}} }\:{dx}\:{but}\: \\ $$$$\sqrt{\mathrm{1}+\xi{x}^{\mathrm{2}} }=\left(\mathrm{1}+\xi{x}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} \:=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\frac{\xi{x}^{\mathrm{2}} }{\mathrm{1}!}\:\:\frac{\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}\right)}{\mathrm{2}!}\:\left(\xi{x}^{\mathrm{2}} \right)^{\mathrm{2}} \:\:\:+{o}\left(\xi\right) \\ $$$$=\mathrm{1}+\frac{\xi{x}^{\mathrm{2}} }{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{8}}\:\xi^{\mathrm{2}} \:{x}^{\mathrm{4}} \:+{o}\left(\xi\right)\:\:\Rightarrow\:\frac{\sqrt{\mathrm{1}+\xi{x}^{\mathrm{2}} }}{{x}^{\mathrm{2}} }\:=\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:+\frac{\xi}{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{8}}\:\xi^{\mathrm{2}} \:{x}^{\mathrm{2}} \:+{o}\left(\xi\right)\:{also} \\ $$$$\frac{\sqrt{\mathrm{1}−\xi{x}^{\mathrm{2}} }}{{x}^{\mathrm{2}} }\:=\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:−\frac{\xi}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{8}}\:\xi^{\mathrm{2}} {x}^{\mathrm{2}} \:+{o}\left(\xi\right)\:\Rightarrow\Rightarrow\frac{\sqrt{\mathrm{1}+\xi{x}^{\mathrm{2}} }+\sqrt{\mathrm{1}−\xi{x}^{\mathrm{2}} }}{\mathrm{2}\xi{x}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\xi{x}^{\mathrm{2}} }\left\{\:\frac{\mathrm{2}}{{x}^{\mathrm{2}} }\:+{o}\left(\xi\right)\right\}\:=\:\frac{\mathrm{1}}{\xi\:{x}^{\mathrm{4}} }\:+{o}\left(\xi\right)\:\Rightarrow\:{I}\left(\xi\right)\:\sim\:\frac{\mathrm{1}}{\xi}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dx}}{{x}^{\mathrm{4}} }\:=\frac{\mathrm{1}}{\xi}\left[\frac{\mathrm{1}}{−\mathrm{4}+\mathrm{1}}\:{x}^{−\mathrm{4}+\mathrm{1}} \right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{3}\xi}\left[\:\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\right]_{\mathrm{0}} ^{\mathrm{1}} \:=\infty \\ $$
