Question Number 121315 by Bird last updated on 06/Nov/20
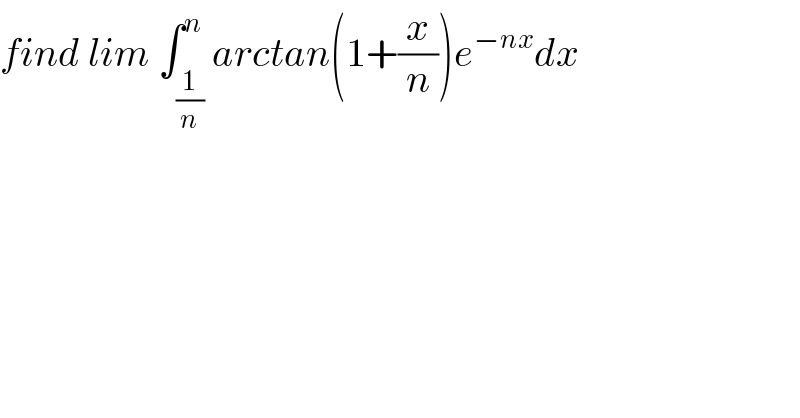
$${find}\:{lim}\:\int_{\frac{\mathrm{1}}{{n}}} ^{{n}} {arctan}\left(\mathrm{1}+\frac{{x}}{{n}}\right){e}^{−{nx}} {dx} \\ $$
Answered by Lordose last updated on 06/Nov/20
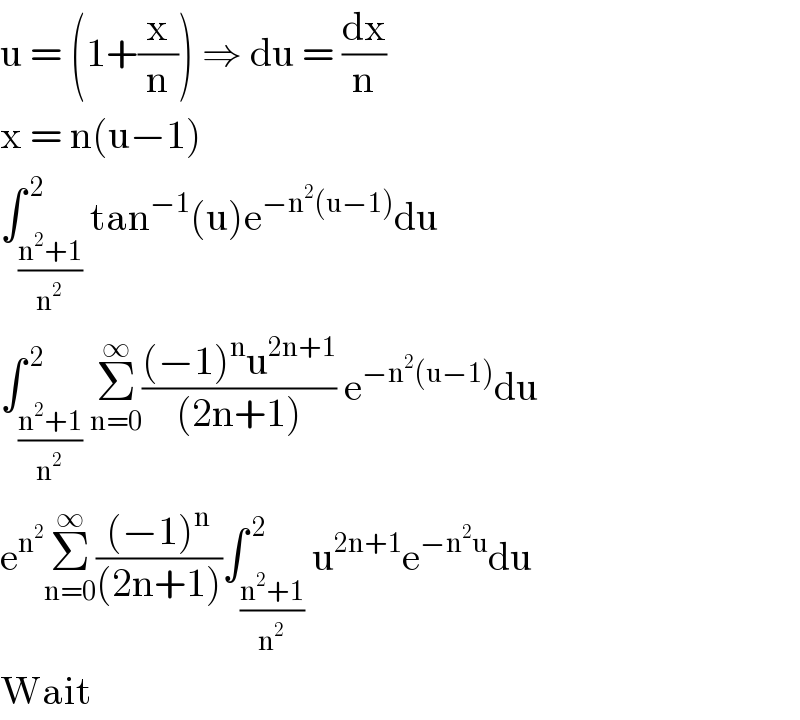
$$\mathrm{u}\:=\:\left(\mathrm{1}+\frac{\mathrm{x}}{\mathrm{n}}\right)\:\Rightarrow\:\mathrm{du}\:=\:\frac{\mathrm{dx}}{\mathrm{n}} \\ $$$$\mathrm{x}\:=\:\mathrm{n}\left(\mathrm{u}−\mathrm{1}\right) \\ $$$$\int_{\frac{\mathrm{n}^{\mathrm{2}} +\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }} ^{\:\mathrm{2}} \mathrm{tan}^{−\mathrm{1}} \left(\mathrm{u}\right)\mathrm{e}^{−\mathrm{n}^{\mathrm{2}} \left(\mathrm{u}−\mathrm{1}\right)} \mathrm{du} \\ $$$$\int_{\frac{\mathrm{n}^{\mathrm{2}} +\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }} ^{\:\mathrm{2}} \underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{u}^{\mathrm{2n}+\mathrm{1}} }{\left(\mathrm{2n}+\mathrm{1}\right)}\:\mathrm{e}^{−\mathrm{n}^{\mathrm{2}} \left(\mathrm{u}−\mathrm{1}\right)} \mathrm{du} \\ $$$$\mathrm{e}^{\mathrm{n}^{\mathrm{2}} } \underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{1}\right)}\int_{\frac{\mathrm{n}^{\mathrm{2}} +\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }} ^{\:\mathrm{2}} \mathrm{u}^{\mathrm{2n}+\mathrm{1}} \mathrm{e}^{−\mathrm{n}^{\mathrm{2}} \mathrm{u}} \mathrm{du} \\ $$$$\mathrm{Wait} \\ $$
Answered by mathmax by abdo last updated on 06/Nov/20
![A_n =∫_(1/n) ^n arctan(1+(x/n))e^(−nx) dx changement (x/n)=t give A_n =∫_(1/n^2 ) ^1 arctan(1+t)e^(−n^2 t) ndt =n ∫_(1/n^2 ) ^1 arctan(1+t)e^(−n^2 t) dt ⇒(A_n /n) =_(by parts) [−(1/n^2 )e^(−n^2 t) arctan(1+t)]_(1/n^2 ) ^1 +(1/n^2 )∫_(1/n^2 ) ^1 (e^(−n^2 t) /(1+(1+t)^2 ))dt =(1/n^2 )e^(−1) arctan(1+(1/n^2 ))−(1/n^2 )e^(−n^2 ) arctan(2)+(1/n^2 )∫_(1/n^2 ) ^1 (e^(−n^2 t) /(1+(1+t)^2 ))dt ⇒ A_n =(1/n)e^(−1) arctan(1+(1/n^2 ))−(1/n)e^(−n^2 ) arctan(2)+(1/n)∫_(1/n^2 ) ^1 (e^(−n^2 t) /(1+(1+t)^2 ))dt we have lim_(n→+∞) (1/n){e^(−1) arctan(1+(1/n^2 ))−e^(−n^2 arctan2) }=0 ∫_(1/n^2 ) ^1 (e^(−n^2 t) /(1+(1+t)^2 ))dt =∫_R f_n (x)dx with f_n (x)=(e^(−n^2 t) /(1+(1+t)^2 )) χ_(](1/n^2 ),1]) (t)dt f_n →^(cs) 0 ⇒(1/n)∫_R f_n (x)dx→0 ⇒lim_(n→+∞) A_n =0](https://www.tinkutara.com/question/Q121343.png)
$$\mathrm{A}_{\mathrm{n}} =\int_{\frac{\mathrm{1}}{\mathrm{n}}} ^{\mathrm{n}} \:\mathrm{arctan}\left(\mathrm{1}+\frac{\mathrm{x}}{\mathrm{n}}\right)\mathrm{e}^{−\mathrm{nx}} \:\mathrm{dx}\:\:\mathrm{changement}\:\frac{\mathrm{x}}{\mathrm{n}}=\mathrm{t}\:\mathrm{give} \\ $$$$\mathrm{A}_{\mathrm{n}} =\int_{\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }} ^{\mathrm{1}} \:\mathrm{arctan}\left(\mathrm{1}+\mathrm{t}\right)\mathrm{e}^{−\mathrm{n}^{\mathrm{2}} \mathrm{t}} \:\:\:\mathrm{ndt}\:=\mathrm{n}\:\:\int_{\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }} ^{\mathrm{1}} \:\mathrm{arctan}\left(\mathrm{1}+\mathrm{t}\right)\mathrm{e}^{−\mathrm{n}^{\mathrm{2}} \mathrm{t}} \:\mathrm{dt} \\ $$$$\Rightarrow\frac{\mathrm{A}_{\mathrm{n}} }{\mathrm{n}}\:=_{\mathrm{by}\:\mathrm{parts}} \:\:\:\:\:\left[−\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\mathrm{e}^{−\mathrm{n}^{\mathrm{2}} \mathrm{t}} \:\mathrm{arctan}\left(\mathrm{1}+\mathrm{t}\right)\right]_{\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }} ^{\mathrm{1}} +\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\int_{\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }} ^{\mathrm{1}} \:\:\frac{\mathrm{e}^{−\mathrm{n}^{\mathrm{2}} \mathrm{t}} }{\mathrm{1}+\left(\mathrm{1}+\mathrm{t}\right)^{\mathrm{2}} }\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\mathrm{e}^{−\mathrm{1}} \:\mathrm{arctan}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\right)−\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\mathrm{e}^{−\mathrm{n}^{\mathrm{2}} } \mathrm{arctan}\left(\mathrm{2}\right)+\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\int_{\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }} ^{\mathrm{1}} \:\frac{\mathrm{e}^{−\mathrm{n}^{\mathrm{2}} \mathrm{t}} }{\mathrm{1}+\left(\mathrm{1}+\mathrm{t}\right)^{\mathrm{2}} }\mathrm{dt}\:\Rightarrow \\ $$$$\mathrm{A}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{n}}\mathrm{e}^{−\mathrm{1}} \:\mathrm{arctan}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\right)−\frac{\mathrm{1}}{\mathrm{n}}\mathrm{e}^{−\mathrm{n}^{\mathrm{2}} } \:\mathrm{arctan}\left(\mathrm{2}\right)+\frac{\mathrm{1}}{\mathrm{n}}\int_{\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }} ^{\mathrm{1}} \:\frac{\mathrm{e}^{−\mathrm{n}^{\mathrm{2}} \mathrm{t}} }{\mathrm{1}+\left(\mathrm{1}+\mathrm{t}\right)^{\mathrm{2}} }\mathrm{dt} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \frac{\mathrm{1}}{\mathrm{n}}\left\{\mathrm{e}^{−\mathrm{1}} \:\mathrm{arctan}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\right)−\mathrm{e}^{−\mathrm{n}^{\mathrm{2}} \:\mathrm{arctan2}} \right\}=\mathrm{0} \\ $$$$\int_{\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }} ^{\mathrm{1}} \:\:\frac{\mathrm{e}^{−\mathrm{n}^{\mathrm{2}} \mathrm{t}} }{\mathrm{1}+\left(\mathrm{1}+\mathrm{t}\right)^{\mathrm{2}} }\mathrm{dt}\:=\int_{\mathrm{R}} \:\mathrm{f}_{\mathrm{n}} \left(\mathrm{x}\right)\mathrm{dx}\:\mathrm{with}\:\mathrm{f}_{\mathrm{n}} \left(\mathrm{x}\right)=\frac{\mathrm{e}^{−\mathrm{n}^{\mathrm{2}} \mathrm{t}} }{\mathrm{1}+\left(\mathrm{1}+\mathrm{t}\right)^{\mathrm{2}} }\:\chi_{\left.\right]\left.\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} },\mathrm{1}\right]} \left(\mathrm{t}\right)\mathrm{dt} \\ $$$$\mathrm{f}_{\mathrm{n}} \rightarrow^{\mathrm{cs}} \:\:\mathrm{0}\:\Rightarrow\frac{\mathrm{1}}{\mathrm{n}}\int_{\mathrm{R}} \mathrm{f}_{\mathrm{n}} \left(\mathrm{x}\right)\mathrm{dx}\rightarrow\mathrm{0}\:\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\mathrm{A}_{\mathrm{n}} =\mathrm{0} \\ $$
