Question Number 55030 by Joel578 last updated on 16/Feb/19
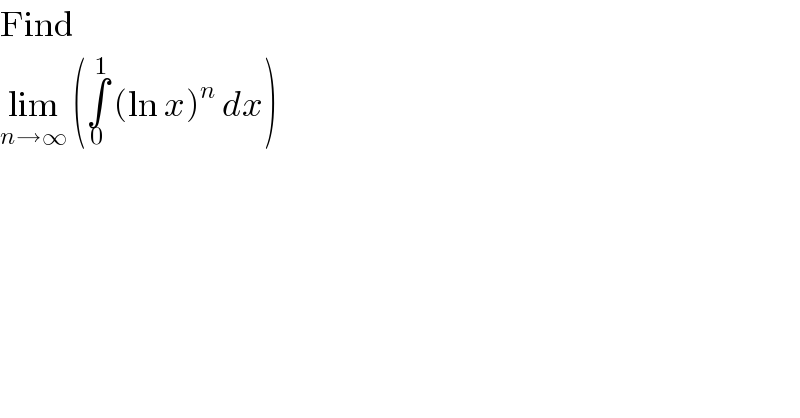
$$\mathrm{Find} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\left(\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\left(\mathrm{ln}\:{x}\right)^{{n}} \:{dx}\right) \\ $$
Commented by tm888 last updated on 16/Feb/19
![is[.]any g.i.f](https://www.tinkutara.com/question/Q55031.png)
$${is}\left[.\right]{any}\:{g}.{i}.{f} \\ $$
Commented by Joel578 last updated on 16/Feb/19
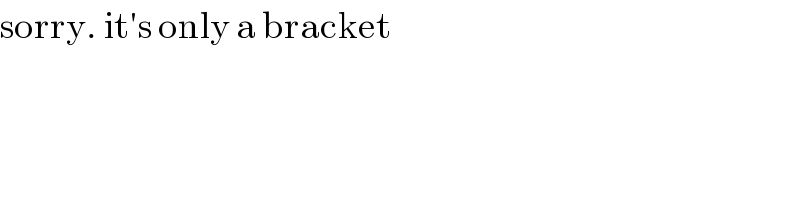
$$\mathrm{sorry}.\:\mathrm{it}'\mathrm{s}\:\mathrm{only}\:\mathrm{a}\:\mathrm{bracket} \\ $$
Commented by tm888 last updated on 16/Feb/19

Commented by maxmathsup by imad last updated on 16/Feb/19
![let A_n =∫_0 ^1 (lnx)^n dx changement ln(x)=−t give x=e^(−t) A_n = ∫_0 ^(+∞) (−t)^n e^(−t) dt =(−1)^n ∫_0 ^∞ t^n e^(−t) dt by parts W_n =∫_0 ^∞ t^n e^(−t) dt =[−t^n e^(−t) ]_0 ^(+∞) +∫_0 ^∞ n t^(n−1) e^(−t) dt =nW_(n−1) ⇒W_n =n! ⇒ A_n =(−1)^n n! ⇒A_(2n) =(2n)! →+∞(n→+∞) and A_(2n+1) =−(2n+1)! →−∞ (n→+∞) so the sequence A_n is divergent . also we can see that ∫_0 ^∞ t^n e^(−t) dt =Γ(n+1)=n!](https://www.tinkutara.com/question/Q55042.png)
$${let}\:{A}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \left({lnx}\right)^{{n}} {dx}\:\:{changement}\:{ln}\left({x}\right)=−{t}\:{give}\:\:{x}={e}^{−{t}} \\ $$$${A}_{{n}} =\:\int_{\mathrm{0}} ^{+\infty} \left(−{t}\right)^{{n}} \:\:{e}^{−{t}} \:{dt}\:=\left(−\mathrm{1}\right)^{{n}} \:\int_{\mathrm{0}} ^{\infty} \:{t}^{{n}} \:{e}^{−{t}} \:{dt}\:\:\:{by}\:{parts}\: \\ $$$${W}_{{n}} =\int_{\mathrm{0}} ^{\infty} \:{t}^{{n}} \:{e}^{−{t}} \:{dt}\:=\left[−{t}^{{n}} \:{e}^{−{t}} \right]_{\mathrm{0}} ^{+\infty} \:+\int_{\mathrm{0}} ^{\infty} \:{n}\:{t}^{{n}−\mathrm{1}} \:\:\:{e}^{−{t}} \:{dt} \\ $$$$={nW}_{{n}−\mathrm{1}} \:\:\:\Rightarrow{W}_{{n}} ={n}!\:\Rightarrow\:{A}_{{n}} =\left(−\mathrm{1}\right)^{{n}} {n}!\:\Rightarrow{A}_{\mathrm{2}{n}} =\left(\mathrm{2}{n}\right)!\:\rightarrow+\infty\left({n}\rightarrow+\infty\right) \\ $$$${and}\:{A}_{\mathrm{2}{n}+\mathrm{1}} =−\left(\mathrm{2}{n}+\mathrm{1}\right)!\:\rightarrow−\infty\:\left({n}\rightarrow+\infty\right)\:{so}\:{the}\:{sequence}\:{A}_{{n}} {is}\:{divergent}\:. \\ $$$${also}\:{we}\:{can}\:{see}\:{that}\:\int_{\mathrm{0}} ^{\infty} \:{t}^{{n}} \:{e}^{−{t}} \:{dt}\:=\Gamma\left({n}+\mathrm{1}\right)={n}! \\ $$
Commented by tm888 last updated on 16/Feb/19
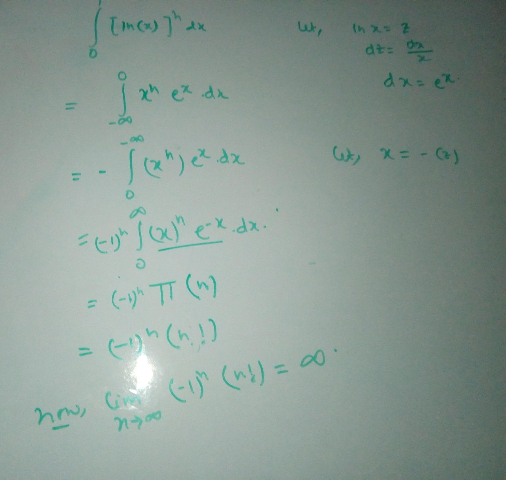
Answered by tanmay.chaudhury50@gmail.com last updated on 16/Feb/19
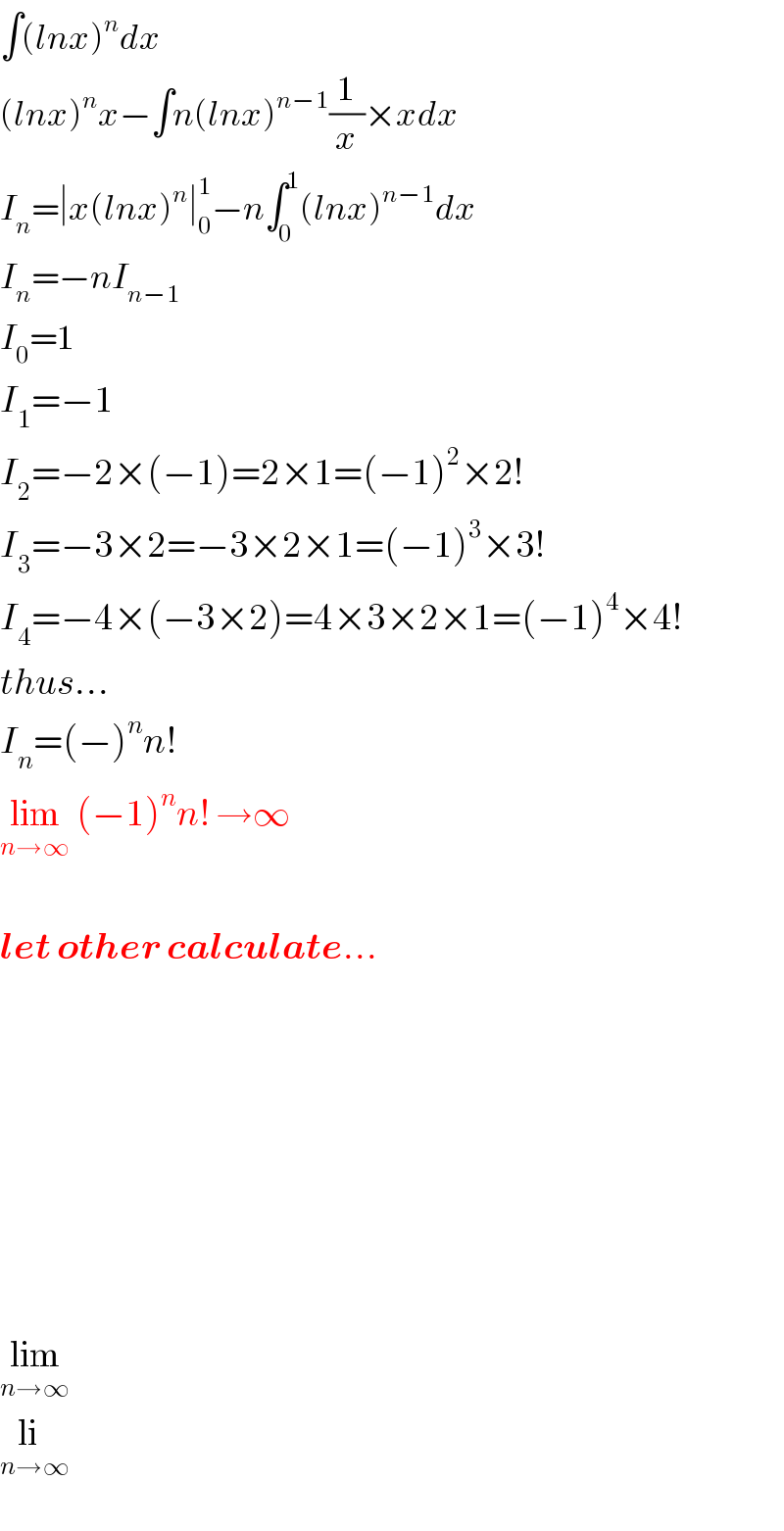
$$\int\left({lnx}\right)^{{n}} {dx} \\ $$$$\left({lnx}\right)^{{n}} {x}−\int{n}\left({lnx}\right)^{{n}−\mathrm{1}} \frac{\mathrm{1}}{{x}}×{xdx} \\ $$$${I}_{{n}} =\mid{x}\left({lnx}\right)^{{n}} \mid_{\mathrm{0}} ^{\mathrm{1}} −{n}\int_{\mathrm{0}} ^{\mathrm{1}} \left({lnx}\right)^{{n}−\mathrm{1}} {dx} \\ $$$${I}_{{n}} =−{nI}_{{n}−\mathrm{1}} \\ $$$${I}_{\mathrm{0}} =\mathrm{1} \\ $$$${I}_{\mathrm{1}} =−\mathrm{1} \\ $$$${I}_{\mathrm{2}} =−\mathrm{2}×\left(−\mathrm{1}\right)=\mathrm{2}×\mathrm{1}=\left(−\mathrm{1}\right)^{\mathrm{2}} ×\mathrm{2}! \\ $$$${I}_{\mathrm{3}} =−\mathrm{3}×\mathrm{2}=−\mathrm{3}×\mathrm{2}×\mathrm{1}=\left(−\mathrm{1}\right)^{\mathrm{3}} ×\mathrm{3}! \\ $$$${I}_{\mathrm{4}} =−\mathrm{4}×\left(−\mathrm{3}×\mathrm{2}\right)=\mathrm{4}×\mathrm{3}×\mathrm{2}×\mathrm{1}=\left(−\mathrm{1}\right)^{\mathrm{4}} ×\mathrm{4}! \\ $$$${thus}… \\ $$$${I}_{{n}} =\left(−\right)^{{n}} {n}! \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\left(−\mathrm{1}\right)^{{n}} {n}!\:\rightarrow\infty \\ $$$$ \\ $$$$\boldsymbol{{let}}\:\boldsymbol{{other}}\:\boldsymbol{{calculate}}… \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{li}} \\ $$
