Question Number 121314 by Bird last updated on 06/Nov/20
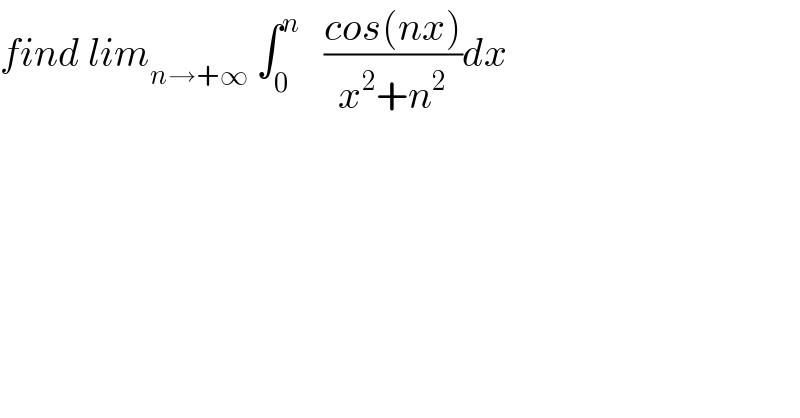
$${find}\:{lim}_{{n}\rightarrow+\infty} \:\int_{\mathrm{0}} ^{{n}} \:\:\:\frac{{cos}\left({nx}\right)}{{x}^{\mathrm{2}} +{n}^{\mathrm{2}} }{dx} \\ $$
Answered by mathmax by abdo last updated on 06/Nov/20

$$\mathrm{I}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{n}} \:\frac{\mathrm{cos}\left(\mathrm{nx}\right)}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{n}^{\mathrm{2}} }\mathrm{dx}\:\:\mathrm{changement}\:\:\mathrm{x}=\mathrm{nt}\:\mathrm{give} \\ $$$$\mathrm{I}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{cos}\left(\mathrm{n}^{\mathrm{2}} \mathrm{t}\right)}{\mathrm{n}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)}\mathrm{ndt}\:=\frac{\mathrm{1}}{\mathrm{n}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{cos}\left(\mathrm{n}^{\mathrm{2}} \mathrm{t}\right)}{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}\mathrm{dt}\:\Rightarrow\mid\mathrm{I}_{\mathrm{n}} \mid\:\leqslant\frac{\mathrm{1}}{\mathrm{n}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$$\mid\mathrm{I}_{\mathrm{n}} \mid\leqslant\frac{\pi}{\mathrm{4n}}\:\rightarrow\mathrm{0}\:\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{I}_{\mathrm{n}} =\mathrm{0} \\ $$
