Question Number 48174 by Abdo msup. last updated on 20/Nov/18
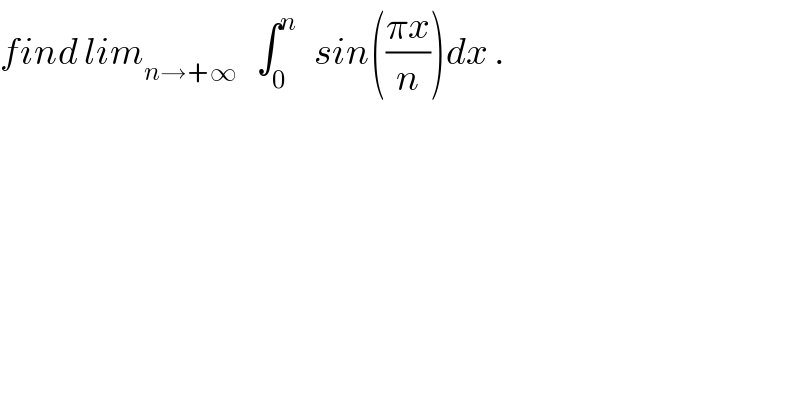
$${find}\:{lim}_{{n}\rightarrow+\infty} \:\:\:\int_{\mathrm{0}} ^{{n}} \:\:\:{sin}\left(\frac{\pi{x}}{{n}}\right){dx}\:. \\ $$
Commented by Abdo msup. last updated on 20/Nov/18
![let A_n =∫_0 ^n sin(((πx)/n))dx ⇒ A_n =[−(n/π)cos(((πx)/n))]_0 ^n =−(n/π){cos(π)−1} =((2n)/π) ⇒ lim_(n→+∞) A_n =+∞](https://www.tinkutara.com/question/Q48210.png)
$${let}\:{A}_{{n}} =\int_{\mathrm{0}} ^{{n}} \:{sin}\left(\frac{\pi{x}}{{n}}\right){dx}\:\Rightarrow \\ $$$${A}_{{n}} =\left[−\frac{{n}}{\pi}{cos}\left(\frac{\pi{x}}{{n}}\right)\right]_{\mathrm{0}} ^{{n}} \:=−\frac{{n}}{\pi}\left\{{cos}\left(\pi\right)−\mathrm{1}\right\} \\ $$$$=\frac{\mathrm{2}{n}}{\pi}\:\Rightarrow\:{lim}_{{n}\rightarrow+\infty} {A}_{{n}} =+\infty\: \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 20/Nov/18
![∫_0 ^n sin(((πx)/n))dx =[((−cos(((πx)/n)))/(π/n))]_0 ^n =((−n)/π)[cosπ−cos0] =((−n)/π)[−2]=((2n)/π) when n→∞ limit also→∞](https://www.tinkutara.com/question/Q48188.png)
$$\int_{\mathrm{0}} ^{{n}} {sin}\left(\frac{\pi{x}}{{n}}\right){dx} \\ $$$$=\left[\frac{−{cos}\left(\frac{\pi{x}}{{n}}\right)}{\frac{\pi}{{n}}}\right]_{\mathrm{0}} ^{{n}} =\frac{−{n}}{\pi}\left[{cos}\pi−{cos}\mathrm{0}\right] \\ $$$$=\frac{−{n}}{\pi}\left[−\mathrm{2}\right]=\frac{\mathrm{2}{n}}{\pi} \\ $$$${when}\:{n}\rightarrow\infty\:{limit}\:{also}\rightarrow\infty \\ $$
