Question Number 35715 by math1967 last updated on 22/May/18
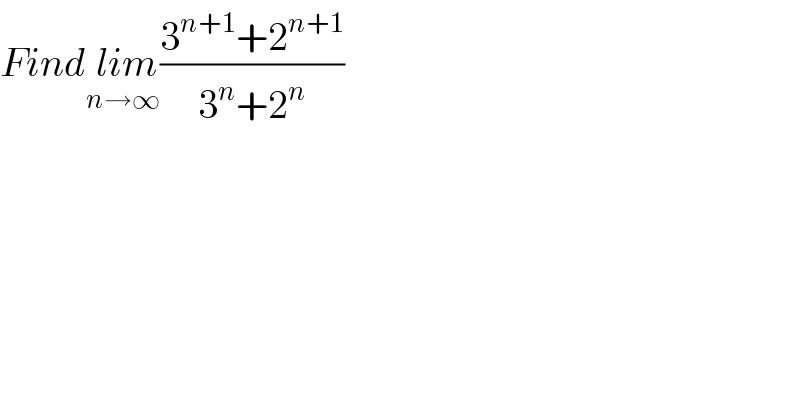
$${Find}\underset{{n}\rightarrow\infty} {\:{lim}}\frac{\mathrm{3}^{{n}+\mathrm{1}} +\mathrm{2}^{{n}+\mathrm{1}} }{\mathrm{3}^{{n}} +\mathrm{2}^{{n}} } \\ $$
Commented by abdo mathsup 649 cc last updated on 22/May/18
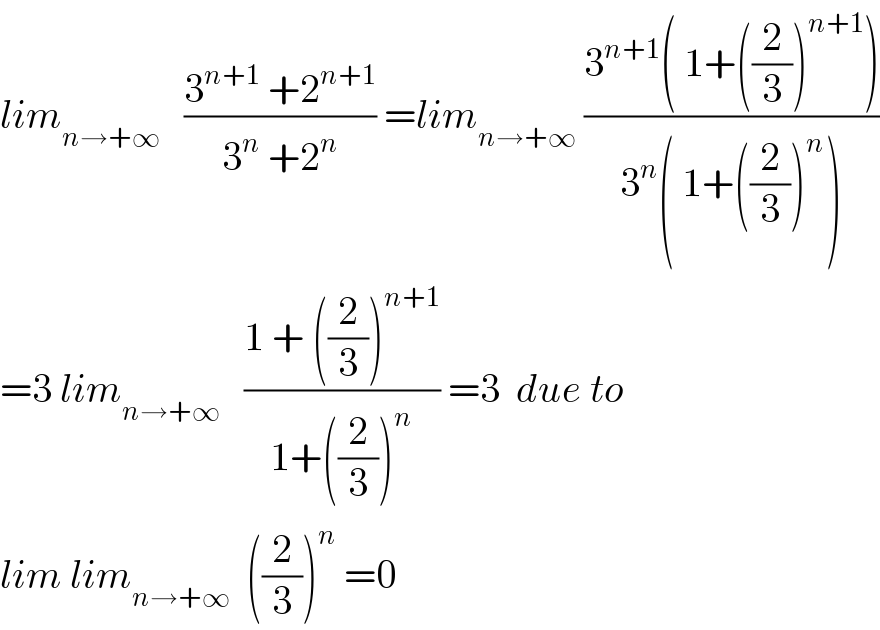
$${lim}_{{n}\rightarrow+\infty} \:\:\:\frac{\mathrm{3}^{{n}+\mathrm{1}} \:+\mathrm{2}^{{n}+\mathrm{1}} }{\mathrm{3}^{{n}} \:+\mathrm{2}^{{n}} }\:={lim}_{{n}\rightarrow+\infty} \:\frac{\mathrm{3}^{{n}+\mathrm{1}} \left(\:\mathrm{1}+\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{n}+\mathrm{1}} \right)}{\mathrm{3}^{{n}} \left(\:\mathrm{1}+\left(\frac{\mathrm{2}}{\mathrm{3}}\underset{} {\right)}^{{n}} \right)} \\ $$$$=\mathrm{3}\:{lim}_{{n}\rightarrow+\infty} \:\:\:\frac{\mathrm{1}\:+\:\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{n}+\mathrm{1}} }{\mathrm{1}+\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{n}} }\:=\mathrm{3}\:\:{due}\:{to} \\ $$$${lim}\:{lim}_{{n}\rightarrow+\infty} \:\:\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{n}} \:=\mathrm{0} \\ $$
Answered by ajfour last updated on 22/May/18
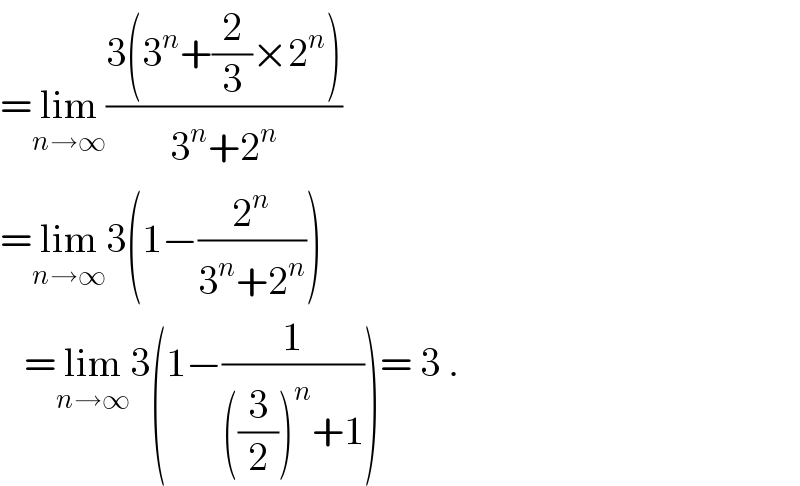
$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{3}\left(\mathrm{3}^{{n}} +\frac{\mathrm{2}}{\mathrm{3}}×\mathrm{2}^{{n}} \right)}{\mathrm{3}^{{n}} +\mathrm{2}^{{n}} } \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}3}\left(\mathrm{1}−\frac{\mathrm{2}^{{n}} }{\mathrm{3}^{{n}} +\mathrm{2}^{{n}} }\right) \\ $$$$\:\:\:=\underset{{n}\rightarrow\infty} {\mathrm{lim}3}\left(\mathrm{1}−\frac{\mathrm{1}}{\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{{n}} +\mathrm{1}}\right)=\:\mathrm{3}\:. \\ $$
