Question Number 26764 by abdo imad last updated on 29/Dec/17
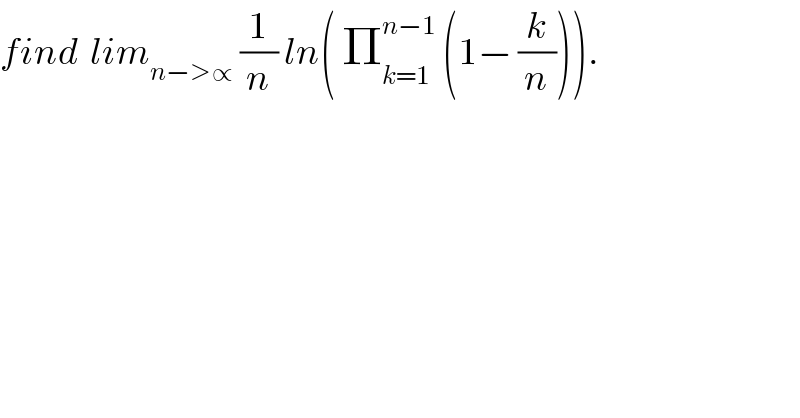
$${find}\:\:{lim}_{{n}−>\propto} \:\frac{\mathrm{1}}{{n}}\:{ln}\left(\:\prod_{{k}=\mathrm{1}} ^{{n}−\mathrm{1}} \:\left(\mathrm{1}−\:\frac{{k}}{{n}}\right)\right). \\ $$
Commented by prakash jain last updated on 29/Dec/17
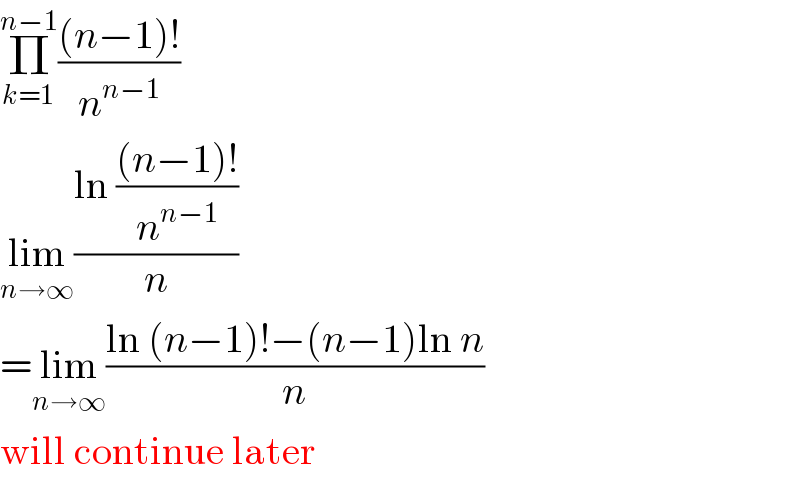
$$\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\prod}}\frac{\left({n}−\mathrm{1}\right)!}{{n}^{{n}−\mathrm{1}} } \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{ln}\:\frac{\left({n}−\mathrm{1}\right)!}{{n}^{{n}−\mathrm{1}} }}{{n}} \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{ln}\:\left({n}−\mathrm{1}\right)!−\left({n}−\mathrm{1}\right)\mathrm{ln}\:{n}}{{n}} \\ $$$$\mathrm{will}\:\mathrm{continue}\:\mathrm{later} \\ $$
Commented by abdo imad last updated on 30/Dec/17
![let remember that if f is Rieman integrable on [a,b] ∫_a ^b f(x)dx = lim_(n−>∝) ((b−a)/n)Σ_(k=0) ^(n−1) f(a +k((b−a)/n) ) so lim_(n−>∝) (1/n) ln( Π_(k=1) ^(k=n) ( 1− (k/n)))=lim_(n−>∝) ((1−0)/n) Σ_(k=1) ^n ln(1−k((1−0)/n)) = ∫_0 ^1 ln(1−x)dx =_(1−x=t) −∫_1 ^0 ln(t)dt = ∫_0 ^1 ln(t)dt =[tln(t)−t]_0 ^1 = −1.](https://www.tinkutara.com/question/Q26879.png)
$${let}\:{remember}\:{that}\:{if}\:{f}\:{is}\:{Rieman}\:{integrable}\:{on}\:\left[{a},{b}\right] \\ $$$$\int_{{a}} ^{{b}} {f}\left({x}\right){dx}\:=\:{lim}_{{n}−>\propto} \:\:\frac{{b}−{a}}{{n}}\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} {f}\left({a}\:+{k}\frac{{b}−{a}}{{n}}\:\right)\:\:{so} \\ $$$${lim}_{{n}−>\propto} \frac{\mathrm{1}}{{n}}\:{ln}\left(\:\prod_{{k}=\mathrm{1}} ^{{k}={n}} \left(\:\mathrm{1}−\:\frac{{k}}{{n}}\right)\right)={lim}_{{n}−>\propto} \frac{\mathrm{1}−\mathrm{0}}{{n}}\:\sum_{{k}=\mathrm{1}} ^{{n}} {ln}\left(\mathrm{1}−{k}\frac{\mathrm{1}−\mathrm{0}}{{n}}\right) \\ $$$$=\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}−{x}\right){dx}\:=_{\mathrm{1}−{x}={t}} −\int_{\mathrm{1}} ^{\mathrm{0}} {ln}\left({t}\right){dt}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left({t}\right){dt}\: \\ $$$$=\left[{tln}\left({t}\right)−{t}\right]_{\mathrm{0}} ^{\mathrm{1}} \:=\:−\mathrm{1}. \\ $$
Commented by prakash jain last updated on 31/Dec/17
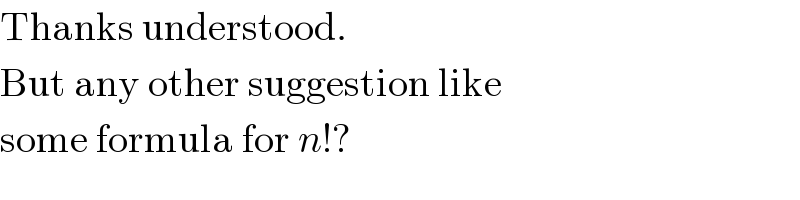
$$\mathrm{Thanks}\:\mathrm{understood}. \\ $$$$\mathrm{But}\:\mathrm{any}\:\mathrm{other}\:\mathrm{suggestion}\:\mathrm{like} \\ $$$$\mathrm{some}\:\mathrm{formula}\:\mathrm{for}\:{n}!? \\ $$
