Question Number 99236 by abdomathmax last updated on 19/Jun/20
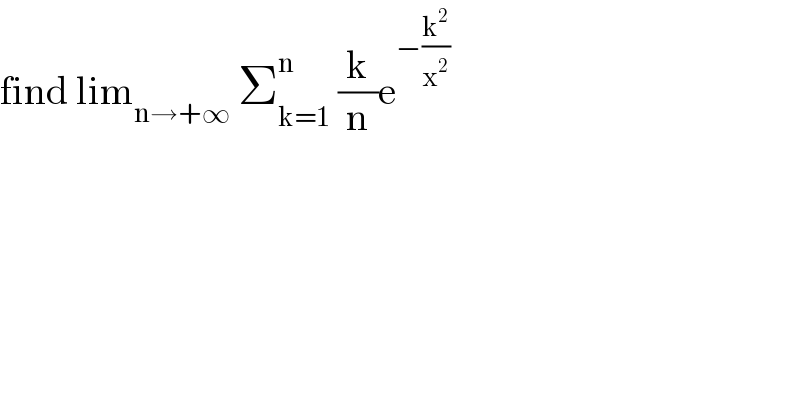
$$\mathrm{find}\:\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{k}}{\mathrm{n}}\mathrm{e}^{−\frac{\mathrm{k}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} }} \\ $$
Commented by Ar Brandon last updated on 19/Jun/20
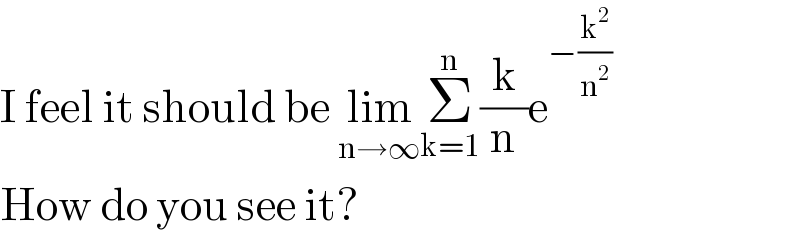
$$\mathrm{I}\:\mathrm{feel}\:\mathrm{it}\:\mathrm{should}\:\mathrm{be}\:\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{k}}{\mathrm{n}}\mathrm{e}^{−\frac{\mathrm{k}^{\mathrm{2}} }{\mathrm{n}^{\mathrm{2}} }} \\ $$$$\mathrm{How}\:\mathrm{do}\:\mathrm{you}\:\mathrm{see}\:\mathrm{it}? \\ $$
Answered by mathmax by abdo last updated on 21/Jun/20

$$\mathrm{sorry}\:\mathrm{the}\:\mathrm{Q}\:\mathrm{is}\:\mathrm{find}\:\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{k}}{\mathrm{n}^{\mathrm{2}} }\mathrm{e}^{−\frac{\mathrm{k}^{\mathrm{2}} }{\mathrm{n}^{\mathrm{2}} }} \\ $$
Answered by Ar Brandon last updated on 21/Jun/20
![l=lim_(n→∞) Σ_(k=1) ^n (k/n)e^(−(k^2 /n^2 )) =lim_(n→∞) n∙(1/n)Σ_(k=1) ^n (k/n)e^(−(k^2 /n^2 )) =lim_(n→∞) n∫_0 ^1 xe^(−x^2 ) dx=lim_(n→∞) −(n/2)∫_0 ^1 −2xe^(−x^2 ) dx =lim_(n→∞) −[(n/2)e^(−x^2 ) ]_0 ^1 =lim_(n→∞) {−(n/2)[(1/e)−1]}=+∞ {(1/e)−1<0}](https://www.tinkutara.com/question/Q99454.png)
$${l}=\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{k}}{\mathrm{n}}\mathrm{e}^{−\frac{\mathrm{k}^{\mathrm{2}} }{\mathrm{n}^{\mathrm{2}} }} =\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}n}\centerdot\frac{\mathrm{1}}{\mathrm{n}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{k}}{\mathrm{n}}\mathrm{e}^{−\frac{\mathrm{k}^{\mathrm{2}} }{\mathrm{n}^{\mathrm{2}} }} \\ $$$$\:\:=\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}n}\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{xe}^{−\mathrm{x}^{\mathrm{2}} } \mathrm{dx}=\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}−\frac{\mathrm{n}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} −\mathrm{2xe}^{−\mathrm{x}^{\mathrm{2}} } \mathrm{dx} \\ $$$$\:\:=\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}−\left[\frac{\mathrm{n}}{\mathrm{2}}\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \right]_{\mathrm{0}} ^{\mathrm{1}} =\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\left\{−\frac{\mathrm{n}}{\mathrm{2}}\left[\frac{\mathrm{1}}{\mathrm{e}}−\mathrm{1}\right]\right\}=+\infty\:\left\{\frac{\mathrm{1}}{\mathrm{e}}−\mathrm{1}<\mathrm{0}\right\} \\ $$
