Question Number 97987 by abdomathmax last updated on 10/Jun/20
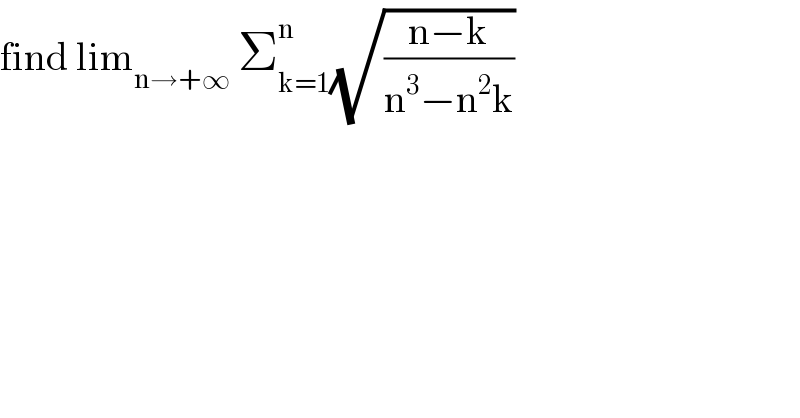
$$\mathrm{find}\:\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \sqrt{\frac{\mathrm{n}−\mathrm{k}}{\mathrm{n}^{\mathrm{3}} −\mathrm{n}^{\mathrm{2}} \mathrm{k}}} \\ $$
Answered by maths mind last updated on 11/Jun/20
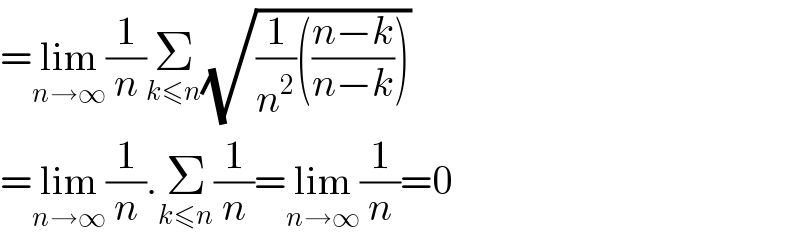
$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{n}}\underset{{k}\leqslant{n}} {\sum}\sqrt{\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\left(\frac{{n}−{k}}{{n}−{k}}\right)} \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{n}}.\underset{{k}\leqslant{n}} {\sum}\frac{\mathrm{1}}{{n}}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{n}}=\mathrm{0} \\ $$
