Question Number 30755 by abdo imad last updated on 25/Feb/18
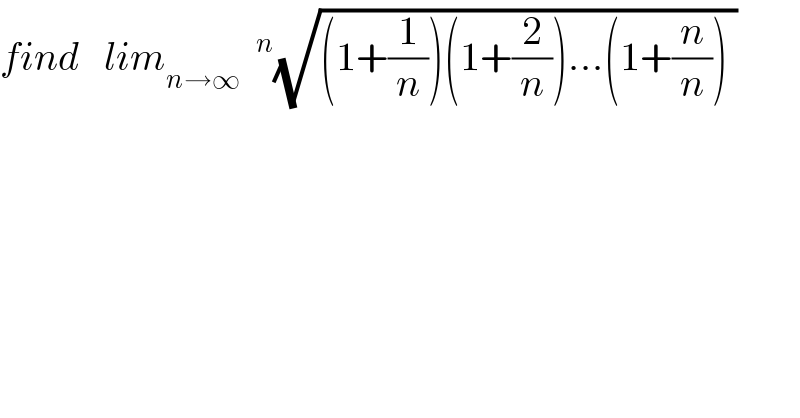
$${find}\:\:\:{lim}_{{n}\rightarrow\infty} \:\:^{{n}} \sqrt{\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)\left(\mathrm{1}+\frac{\mathrm{2}}{{n}}\right)…\left(\mathrm{1}+\frac{{n}}{{n}}\right)\:} \\ $$
Commented by abdo imad last updated on 28/Feb/18
![let put A_n =^n (√((1+(1/n))(1+(2/n))....(1+(n/n)))) we have ln(A_n )= (1/n) ln(Π_(k=1) ^n (1+(k/n)))=(1/n) Σ_(k=1) ^n ln(1+(k/n))so ln(A_n ) is a Rieman sum and lim_(n→∞) ln(A_n ) = ∫_0 ^1 ln(1+x)dx= ∫_1 ^2 ln(t)dt=[tlnt −t]_1 ^2 =2ln2−2 +1=2ln2 −1 ⇒lim_(n→∞) A_n = e^(−1) e^(ln(4)) =(4/e) .](https://www.tinkutara.com/question/Q30907.png)
$${let}\:{put}\:{A}_{{n}} =^{{n}} \sqrt{\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)\left(\mathrm{1}+\frac{\mathrm{2}}{{n}}\right)….\left(\mathrm{1}+\frac{{n}}{{n}}\right)}\:\:\:{we}\:{have} \\ $$$${ln}\left({A}_{{n}} \right)=\:\frac{\mathrm{1}}{{n}}\:{ln}\left(\prod_{{k}=\mathrm{1}} ^{{n}} \left(\mathrm{1}+\frac{{k}}{{n}}\right)\right)=\frac{\mathrm{1}}{{n}}\:\sum_{{k}=\mathrm{1}} ^{{n}} \:{ln}\left(\mathrm{1}+\frac{{k}}{{n}}\right){so} \\ $$$${ln}\left({A}_{{n}} \right)\:{is}\:{a}\:{Rieman}\:{sum}\:{and}\:{lim}_{{n}\rightarrow\infty} {ln}\left({A}_{{n}} \right) \\ $$$$=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{ln}\left(\mathrm{1}+{x}\right){dx}=\:\int_{\mathrm{1}} ^{\mathrm{2}} \:{ln}\left({t}\right){dt}=\left[{tlnt}\:−{t}\right]_{\mathrm{1}} ^{\mathrm{2}} \\ $$$$=\mathrm{2}{ln}\mathrm{2}−\mathrm{2}\:+\mathrm{1}=\mathrm{2}{ln}\mathrm{2}\:−\mathrm{1}\:\Rightarrow{lim}_{{n}\rightarrow\infty} {A}_{{n}} =\:{e}^{−\mathrm{1}} \:{e}^{{ln}\left(\mathrm{4}\right)} \:=\frac{\mathrm{4}}{{e}}\:. \\ $$
