Question Number 29511 by abdo imad last updated on 09/Feb/18
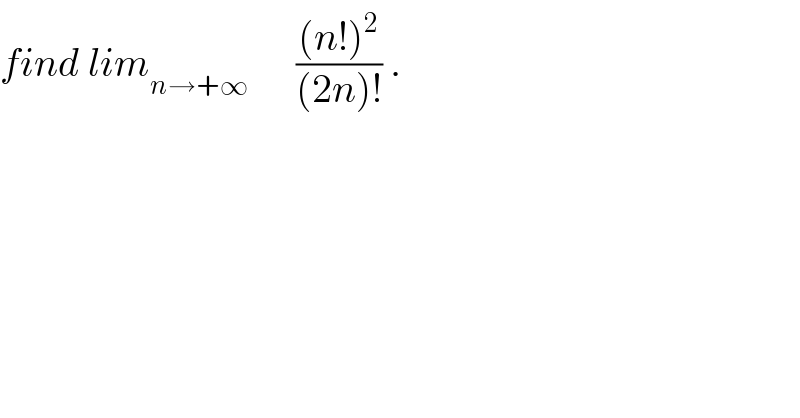
$${find}\:{lim}_{{n}\rightarrow+\infty} \:\:\:\:\:\:\frac{\left({n}!\right)^{\mathrm{2}} }{\left(\mathrm{2}{n}\right)!}\:. \\ $$
Commented by prof Abdo imad last updated on 12/Feb/18
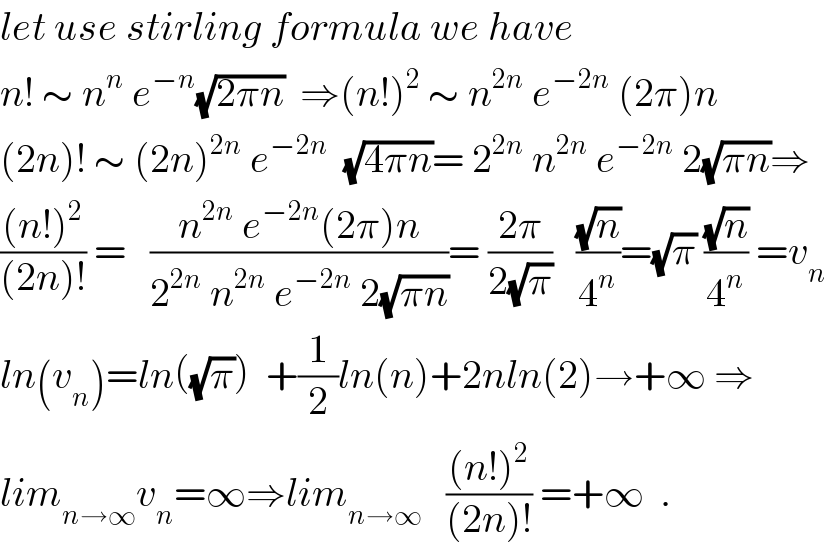
$${let}\:{use}\:{stirling}\:{formula}\:{we}\:{have} \\ $$$${n}!\:\sim\:{n}^{{n}} \:{e}^{−{n}} \sqrt{\mathrm{2}\pi{n}}\:\:\Rightarrow\left({n}!\right)^{\mathrm{2}} \:\sim\:{n}^{\mathrm{2}{n}} \:{e}^{−\mathrm{2}{n}} \:\left(\mathrm{2}\pi\right){n} \\ $$$$\left(\mathrm{2}{n}\right)!\:\sim\:\left(\mathrm{2}{n}\right)^{\mathrm{2}{n}} \:{e}^{−\mathrm{2}{n}} \:\:\sqrt{\mathrm{4}\pi{n}}=\:\mathrm{2}^{\mathrm{2}{n}} \:{n}^{\mathrm{2}{n}} \:{e}^{−\mathrm{2}{n}} \:\mathrm{2}\sqrt{\pi{n}}\Rightarrow \\ $$$$\frac{\left({n}!\right)^{\mathrm{2}} }{\left(\mathrm{2}{n}\right)!}\:=\:\:\:\frac{{n}^{\mathrm{2}{n}} \:{e}^{−\mathrm{2}{n}} \left(\mathrm{2}\pi\right){n}}{\mathrm{2}^{\mathrm{2}{n}} \:{n}^{\mathrm{2}{n}} \:{e}^{−\mathrm{2}{n}} \:\mathrm{2}\sqrt{\pi{n}}}=\:\frac{\mathrm{2}\pi}{\mathrm{2}\sqrt{\pi}}\:\:\:\frac{\sqrt{{n}}}{\mathrm{4}^{{n}} }=\sqrt{\pi}\:\frac{\sqrt{{n}}}{\mathrm{4}^{{n}} }\:={v}_{{n}} \\ $$$${ln}\left({v}_{{n}} \right)={ln}\left(\sqrt{\pi}\right)\:\:+\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({n}\right)+\mathrm{2}{nln}\left(\mathrm{2}\right)\rightarrow+\infty\:\Rightarrow \\ $$$${lim}_{{n}\rightarrow\infty} {v}_{{n}} =\infty\Rightarrow{lim}_{{n}\rightarrow\infty} \:\:\:\frac{\left({n}!\right)^{\mathrm{2}} }{\left(\mathrm{2}{n}\right)!}\:=+\infty\:\:. \\ $$
