Question Number 33168 by abdo imad last updated on 11/Apr/18
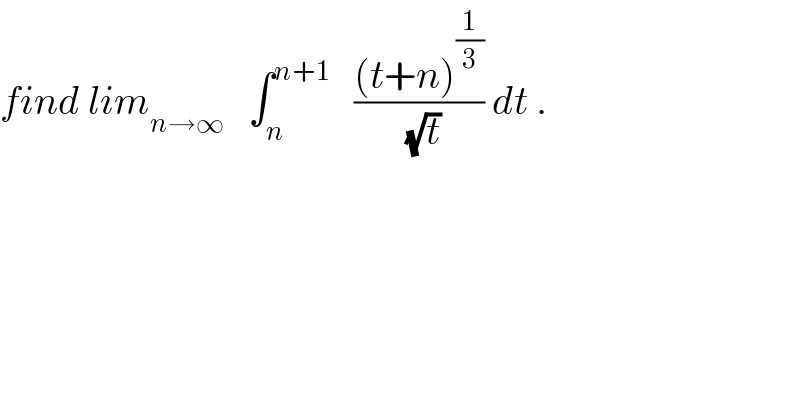
$${find}\:{lim}_{{n}\rightarrow\infty} \:\:\:\int_{{n}} ^{{n}+\mathrm{1}} \:\:\:\frac{\left({t}+{n}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} }{\:\sqrt{{t}}}\:{dt}\:. \\ $$
Commented by abdo imad last updated on 13/Apr/18
![∃ξ∈]n,n+1[ /I_n = ∫_n ^(n+1) (((t +n)^(1/3) )/( (√t)))dt =^3 (√(ξ +n)) ∫_n ^(n+1) (dt/( (√t))) =^3 (√(ξ +n)) [2(√(t])) _n^(n+1) = 2^3 (√(n+ξ)) ((√(n+1)) −(√n) ) = ((2^3 (√(n+ξ)))/( (√(n+1)) +(√n))) ∼ ((2(2n)^(1/3) )/(2(√n))) =^3 (√3) n^((1/3)−(1/2)) =^3 (√2) n^(−(1/6)) →0(n→∞) so lim_(n→∞) I_n =0 .](https://www.tinkutara.com/question/Q33246.png)
$$\left.\exists\xi\in\right]{n},{n}+\mathrm{1}\left[\:\:/{I}_{{n}} =\:\int_{{n}} ^{{n}+\mathrm{1}} \:\:\:\frac{\left({t}\:+{n}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} }{\:\sqrt{{t}}}{dt}\right. \\ $$$$=^{\mathrm{3}} \sqrt{\xi\:+{n}}\:\int_{{n}} ^{{n}+\mathrm{1}} \:\frac{{dt}}{\:\sqrt{{t}}}\:\:=\:^{\mathrm{3}} \sqrt{\xi\:+{n}}\:\left[\mathrm{2}\sqrt{\left.{t}\right]}\:_{{n}} ^{{n}+\mathrm{1}} \right. \\ $$$$=\:\mathrm{2}^{\mathrm{3}} \sqrt{{n}+\xi}\:\left(\sqrt{{n}+\mathrm{1}}\:−\sqrt{{n}}\:\right)\:=\:\frac{\mathrm{2}^{\mathrm{3}} \sqrt{{n}+\xi}}{\:\sqrt{{n}+\mathrm{1}}\:\:+\sqrt{{n}}} \\ $$$$\:\sim\:\:\frac{\mathrm{2}\left(\mathrm{2}{n}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} }{\mathrm{2}\sqrt{{n}}}\:=^{\mathrm{3}} \sqrt{\mathrm{3}}\:\:{n}^{\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{2}}} \:=^{\mathrm{3}} \sqrt{\mathrm{2}}\:\:{n}^{−\frac{\mathrm{1}}{\mathrm{6}}} \:\rightarrow\mathrm{0}\left({n}\rightarrow\infty\right)\:{so} \\ $$$${lim}_{{n}\rightarrow\infty} \:\:{I}_{{n}} \:\:=\mathrm{0}\:\:. \\ $$
